Didácticos
ENLACE 2011 se acerca (prepárate desde hoy)
En este post se discuten cuatro problemas de geometría analítica de ENLACE 2010 y se recomiendan algunas estrategias de resolución que han probado su eficacia en la práctica.
ENLACE bachillerato (vive la experiencia on line)
En estos días me puse a resolver el examen en línea ENLACE Bachillerato 2010 y puedo decirles que no está de "enchílame otra". Para empezar les diré que es excesivamente largo: me tomó todo un día resolverlo (dentro de la rutina hogareña de un domingo --es decir, con salidas al centro, visitas, etc.).
Ecuación de la recta
Tres conceptos básicos de la geometría analítica
Con trigonometría (a veces) la creatividad es innecesaria
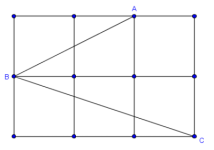
Hablando en general, la solución de un problema de geometría exige cierta creatividad. Ésta, con frecuencia, consiste en ver el problema de otra forma. Por ejemplo, ampliando el contexto mediante un trazo auxiliar.
Se trata del fenómeno del framing el cual he abordado en otros posts en MaTeTaM. Framing se traduce como encuadre o enmarcamiento, como cuando se le pone el marco a una fotografía o pintura. Así pues, la creatividad, con frecuencia, consiste en poner al problema en un marco adecuado.
Problemas con trampa procedimental
La pregunta clásica de Sócrates, que conduce al alumno a una falsa respuesta, está orientada a que el interlocutor vea de bulto que su tesis es insostenible. Para Sócrates era rutina, pero...
Más allá del procedimiento
El diseño de problemas no rutinarios como una forma de que el aprendiz aprenda y/o refuerce el significado de ciertos conceptos matemáticos clave es una tarea que lleva tiempo. Pero, además, el diseñador debe conocer el principio general de diseño: el problema debe incluir una trampa procedimental, y ésta debe propiciar el asombro de quien caiga en ella al descubrir que algo está mal en su procedimiento.
Grafos --caminos, ciclos, conexidad
En este post voy a presentar otro grupo de conceptos de la teoría de grafos, ligados a la noción de camino --la metáfora obvia es un mapa de carreteras. El significado usual de camino es una vía, una ruta, por la que se transita para ir de un lugar geográfico a otro --quizá pasando por otros lugares. El significado es tan básico que su definición sale sobrando. En teoría de grafos
Grafos --incidencia, grado de un vértice, y un teorema de Euler
Como se sabe, un grafo $G$ consiste de vértices y aristas, donde éstas se pueden ver como pares de vértices. El conjunto de vértices suele denotarse con $V$ y el de aristas con $E$ --y el grafo con $G(V,E)$. Como ya se dijo en el post Modelación de Relaciones, la utilidad principal de los grafos es la modelación de relaciones.

Grafos --y la modelación de relaciones
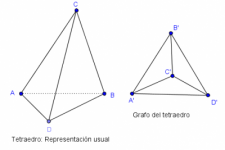
En este post la noción matemática de grafo es presentada a través de la metáfora de los poliedros y la relación de adyacencia entre sus vértices. Y ello para darle la vuelta a las definiciones formales, y ahorrarnos al menos cuatro definiciones: vértice, arista, la relación de adyacencia entre vértices, y la de incidencia entre vértices y aristas.
La dialéctica entre técnica y teoría
La dialéctica es un método de razonamiento que se basa en la contradicción: cada afirmación (tesis) tiene una antítesis que la contradice; y del enfrentamiento entre ambas surge una síntesis que elimina la contradicción (y la síntesis se convierte en la nueva tesis que encontrará su antítesis, etc.)
¿Es el aprendizaje del álgebra un problema resoluble con tecnología?
La computadora, se ha dicho, es una solución en busca de problemas. Y en la enseñanza de las matemáticas se postuló, desde la aparición de esa herramienta maravillosa, que la PC (y, antes de ella, las calculadoras) podría ser la solución a las dificultades que los estudiantes enfrentan al aprender esa "ciencia incomprensible" (la etiqueta es espuria, pero de aceptación universal) denominada álgebra .
