La respuesta a la pregunta del título es: depende del razonador. Esta respuesta la derivé de una experiencia de enseñanza que a continuación narro y comento.
En estos días, dentro del tema de geometría, traté de enseñarles a dos jóvenes universitarios el teorema de Pitágoras. Es decir, la demostración de ese famoso teorema. Fue de hecho un experimento didáctico, solamente para comprobar que a un estudiante profesional (es decir, que el ser estudiante ha sido su modus vivendi por al menos 13 años) le resulta casi imposible concentrarse en una tarea de este tipo.
Una primera sorpresa fue que no lo conocían, es decir, ni siquiera habían oído hablar de él. Así que tuve que entrar a explicarles, previo al enunciado del teorema, los triángulos rectángulos, cateto, hipotenusa, el cuadrado de un número, áreas de un triángulo, de un cuadrado, etc. (Cosas que tampoco sabían o ya se les habían olvidado.)
Como se sabe, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Éste es el Teorema de Pitágoras. La demostración más sencilla del Teorema de Pitágoras se basa en el diagrama siguiente.
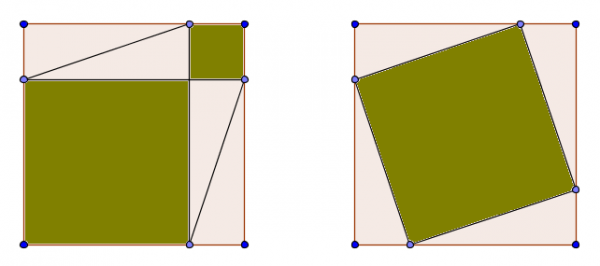
Les mostré este diagrama y, sin muchas esperanzas, les di la consigna de que lo miraran un buen rato a ver si se les ocurría la relación de ese diagrama con el teorema de Pitágoras. Después de 10 o 15 minutos les di una ayuda socrática:
jmd: ¿pueden ver, muchachos, que estas dos figuras son iguales?
Estudiantes: Sí, profe.
jmd: En el cuadrado de la izquierda los triángulos allí formados son iguales que los triángulos del cuadrado de la derecha ¿pueden ver eso?
Estudiantes: Ciertamente, profe.
jmd: Y si a cada uno de los cuadrados le quitamos los cuatro triángulos…
En este punto, mi fantasía era que alguno de ellos dijera:
¡Profe! ¡Es el teorema de Pitágoras! Deje y se lo explico. Como los dos cuadrados grandes son iguales, entonces tienen la misma área. Y como los cuatro triángulos en cada uno de ellos son correspondientemente iguales, entonces le estaría quitando a cada uno de los cuadrados una misma cantidad en área. De ahí se sigue que el cuadrado que queda en el diagrama de la izquierda tiene la misma área que los dos cuadrados que quedan en el diagrama de la derecha. ¿Puede verlo, profe?
Pero mi fantasía se quedó en eso, pues los chicos no avanzaron más allá de reconocer las igualdades de las figuras sobre las cuales les llamé la atención antes.
Después insistí: "¿que pasaría si quitamos los cuatro triángulos rectángulos de cada cuadrado?"
Ellos se quedaron pensando y después uno dijo: "pues quedarían en éste el cuadrado central y en este otro dos cuadrados, uno pequeño y otro más grande."
Y yo dije: "¿es todo?" (Se me quedaron mirando confundidos o fastidiados...)
Debo aclarar que las figuras tenían etiquetados los lados (con $a$ uno de los catetos, con $b$ el otro y con $c$ la hipotenusa) --las había dibujado en el pizarrón.
Yo les dije: "¿pueden calcular el área de las figuras resultantes después de retirar los triángulos rectángulos?"
"Claro que sí profe, pero nos tiene que dar los datos"
En ese momento suspendí la sesión, un tanto decepcionado, y porque el tiempo se estaba agotando... Me dí cuenta de que se necesitarían más de dos sesiones para terminar el experimento. Les dejé de tarea que hicieran un poster de la figura y otro donde se han retirado los triángulos rectángulos de los cuadrados iguales. (Y bueno, mejor ya no les cuento que a la siguiente sesión ninguno había hecho la tarea. Concluí que lo más fácil es enseñar --como todo mundo lo hace-- las fórmulas del área de figuras y del volumen de sólidos. Estas enseñanzas se adaptan mucho mejor a nuestros estudiantes contemporáneos y al tiempo del aula.)
De cualquier manera permítaseme el siguiente comentario sobre el muchacho de mi fantasía y su razonamiento con el diagrama (el sistema cognitivo muchacho-diagramas):
1. El muchacho (el aprendiz) debe interactuar cognitivamente con el diagrama. Y, para ello, necesita tener conocimientos de geometría. Ello significaría que hizo todas las tareas en la secundaria --si es que le tocaron buenos profesores...
2. Pero dichos conocimientos no son suficientes. El muchacho debe tener un interés real en interpretar toda la situación didáctica planteada por el diagrama (y el profesor). La situación no debe serle indiferente. (Lo cual es altamente improbable en nuestras aulas contemporáneas.)
Después de que la sesión terminó consulté el Google: en español aparecen 184 000 páginas para Pitágoras. Este número es muy pequeño. Porque, por ejemplo, para Grupo Pesado el número es de 5 800 000. (Y para no te la vas a acabar son 6 630 000 páginas encontradas por Google.)
Yo me quedé con un sentimiento de culpa debido a que el teorema de Pitágoras no les sirve de nada a los estudiantes. Digo, en el sentido de ganar dinero, por ejemplo. Y los profesores de matemáticas --y los programas-- son tercos en querer enseñar lo que ninguna utilidad tiene. Como se sabe, es un valor entendido (i.e., todo mundo lo sabe excepto quienes hacen los programas) en la cultura escolar de los docentes que el tema de geometría incluye áreas de polígonos y volúmenes de sólidos y es todo (bueno, no es todo pero como ya se acabó el semestre pues... )
Y también pude extraer la siguiente moraleja: el aprendiz no sabe leer el diagrama porque nunca se lo han enseñado; la prueba visual no es evidente, como sostienen quienes hicieron su tesis doctoral en razonamiento diagramático. Es decir, solamente es evidente cuando uno ya aprendió a leer el diagrama --para el cazador es evidente que una huella es de venado (o de jabalí o etc.), pero para que llegue a serle evidente tuvo que pasar un período de aprendizaje...
Los saluda
jmd
PD: es posible que el lector encuentre interesante observar que una de las 8 competencias matemáticas que se están planteando para bachillerato en la RIEMS es : Interpreta tablas, gráficas, mapas, diagramas y textos con símbolos matemáticos y científicos. Ver mi post sobre ese tema
