En este post voy a argumentar a favor del uso de los vectores en el problem solving en geometría. Con las definiciones iniciales de vector, vectores de posición, vectores libres, igualdad de vectores, y la suma y resta de vectores presento la demostración de varios teoremas de la geometría como instancias de uso de esta poderosa herramienta. Destacan las instancias de uso finales sobre la demostración puramente vectorial de la fórmula de Sylvester y de la Recta de Euler.
Espero con esta presentación poder convencer a los novicios con mayor nivel de aspiración en los concursos de matemáticas a que se apropien de la herramienta vectorial para resolver problemas de geometría. Para la composición de este post he hecho una investigación del material disponible en la Web y les puedo decir que el material (al nivel que lo presento aquí) es muy escaso. Lo que abunda es material demasiado elemental o bien muy avanzado.
Sobre el concepto de vector en geometría plana
En geometría, un vector está asociado a una traslación o desplazamiento de una configuración geométrica. Trasladar un triángulo según el vector (4,-9) significa que todos los puntos del triángulo se desplazan 4 unidades a la derecha y 9 hacia hacia abajo. El vector así entendido es un vector de desplazamiento o vector de traslación.
Esta es la interpretación preferente de vector en geometría: un vector es un vector de desplazamiento. En sentido estricto es desplazamiento paralelo --al vector. (En geometría euclideana, una traslación del plano o de una figura geométrica es una función que mueve cada punto una distancia constante en una dirección especificada. En términos de vectores, una traslación se representa como la adición o suma de un vector constante a cada punto de la figura.)
La definición general de vector como cantidad con magnitud y dirección, está orientada a incluir sus aplicaciones en la física: una fuerza, una velocidad, en física son cantidades con magnitud y dirección. Notemos, de paso, que un vector --en ambas definiciones-- lleva consigo dos informaciones: una dirección y una magnitud.
Pero la definición general de vector queda incluida en la definición geométrica: un vector es un par ordenado de números reales. La definición general de vector queda incluida en su definición geométrica pues ésta hace referencia de manera implícita a un sistema de coordenadas. Y tiene la ventaja de que, con ella, es muy fácil definir la suma y la diferencia de vectores: $(a,b)+(c,d)=(a+c,b+d) y (a,b)-(c,d)=(a-c,b-d)$. Y le da un sentido a la suma y a la diferencia de puntos en el plano cartesiano.
La definición de vector como par ordenado de números reales está ligada o atada a un sistema cartesiano de coordenadas y podría parecer limitada pero es la más económica (en un sentido cognitivo). Pues partir de esta definición básica, la cual se refiere en sentido estricto a un vector en posición estándar (con origen en el origen de coordenadas), se puede pasar al concepto de vector libre (y al concepto general de vector en geometría como una clase de equivalencia).
Igualdad de vectores: se dice que dos vectores son iguales si tienen la misma dirección y la misma magnitud. Por ejemplo, el vector (6,4) es igual al vector que tiene su origen en A=(2,3) y su punto terminal en B=(8,7). Pues ambos tienen la misma dirección (determinada por la tangente del ángulo que forman con el eje X) y la misma magnitud (la distancia euclideana entre sus extremos). Notemos que la diferencia $B-A=(8-2,7-3)=(6,4).$
Una de las claves que abren la caja de herramienta de los vectores es llegar a ver (y a aceptar) que todos los vectores iguales (tambien se les llama equipolentes) tienen como representante principal a un vector en posición estándar.
(El aprendiz aceptará más fácilmente esta forma de ver los vectores si la compara con los números racionales: 2/3, 4/6 y 16/24 es un mismo número y su representación estándar es la fracción simplificada 2/3. "¿Cómo que son iguales? ¡Pero si yo los veo que son diferentes!")
Otro obstáculo epistemológico que cierra la entrada a la caja fuerte de los vectores es la negativa del aprendiz a ver un punto en el plano como vector. ("¡O es punto o es vector!¡No puede ser ambas cosas!)
Una forma de llegar a aceptar esa dualidad de significado es, quizá, a través de las operaciones que se pueden efectuar con cada uno: con los puntos no tienen mucho sentido la suma y la diferencia --porque no son útiles--, pero con los vectores adquieren un sentido poderoso en el problem solving.
A la manera de las imágenes duales de la Gestalt (percepción de la forma total), no es posible ver ambos significados a la vez, pero sí se puede switchear de uno al otro.

A un vector que no está en posición estándar se le llama vector libre. (Pero, se entiende que puede ser convertido a uno igual a él en posición estándar.)
En un sistema cartesiano de coordenadas, el vector libre se debe interpretar como un desplazamiento que va del punto inicial del vector a su punto terminal. Y, en esta interpretación, el punto terminal se encuentra ligado al punto inicial --como si el punto inicial fuese el origen de coordenadas.
En este sentido es fácil entender el hecho (o la definición) de que el vector libre AB sea equivalente (o igual) al vector de posición B-A. Pues para llegar a B desde A es necesario un desplazamiento de acuerdo al vector libre AB.
Es decir, B=A+AB. He aquí otra dualidad de conveniencia: usamos vectores libres cuando solamente la magnitud y la dirección son importantes en el problema a resolver --y se puede pasar de una forma a otra si así es conveniente.
Incluso sin un sistema dado de coordenadas, siempre se puede postular un origen O de coordenadas y... bueno, mejor vean las instancias de uso de abajo.
Representación gráfica: un vector se representa gráficamente como una flecha (segmento de recta con punta de flecha) donde se debe entender que la punta de la flecha es el punto terminal del vector y el otro extremo es su punto inicial u origen. La flecha conecta el punto inicial, digamos A, con su punto terminal, digamos B. Se denota con AB con una flecha encima.
Geométricamente, y con esta representación gráfica, se puede redefinir de manera equivalente la noción de igualdad de vectores:
Dos vectores AB y A'B'son iguales si ABB'A' es un paralelogramo.
Y también la suma de vectores:
La suma de dos vectores en posición estándar A y B es la diagonal del paralelogramo definido por el origen O y los puntos A y B. El cuarto vértice del paralelogramo es la suma A+B.
La regla del paralelogramo para la suma de vectores tiene una interpretación en términos de desplazamientos: si uno se mueve primero del origen al punto A y después desde A, en la dirección de B, tantas unidades como la longitud de B, llegaremos al punto A+B. (Notemos que el resultado es el mismo si nos movemos del origen a B y despues desde B y en la dirección de A tantas unidades como la longitud de A.)
Con estos pocos conceptos y operaciones (vector, vector en posición estándar, vectores libres, igualdad de vectores, y suma y resta de vectores) ya se puede pasar a ver
Algunas instancias de uso
Teorema de la línea media: Sea $ABC$ un triángulo y $M$ y $N$ los puntos medios de los lados $AB$ y $AC$, respectivamente. Entonces $MN$ es paralela a la base y mide la mitad de ésta.
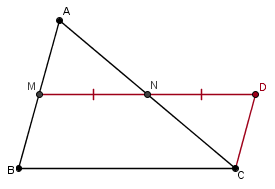
Demostración vectorial
MN=AN-AM=1/2(AB-AC)=1/2(B-A-C+A)=1/2(B-C)=1/2(BC).
Coordenadas del punto medio: Las coordenadas del punto medio M del segmento AB son el promedio de las coordenadas de sus extremos.
Demostración vectorial
Sean O el origen de coordenadas y A y B los vectores de posición correspondientes a los puntos A y B, respectivamente. Entonces la suma vectorial A+B corresponde al extremo de la diagonal por O del paralelogramo definido por O, A, B. Pero las diagonales de un paralelogramo se bisecan. Por tanto, el punto medio del vector AB son las de 1/2(A+B).
Coordenadas del baricentro: Las coordenadas del baricentro de un triángulo ABC son el promedio de las coordenadas de sus vértices.
Demostración vectorial
Denotemos con $A´,B',C'$ los puntos medios de los lados $BC,CA, AB$, respectivamente, y con $G$ el baricentro. Como se acaba de demostrar, $AA'=1/2(AB+AC)$.
Y, como sabemos, el baricentro $G$ se encuentra a 2/3 de la distancia de $A$ a $A'$. Por tanto, $AG=2/3(AA')=2/3(1/2)(AB+AC)$. Pasando a vectores en posición estándar se tiene: $3(G-A)=B-A+C-A$. Es decir, $3G=A+B+C$.
Vectores del baricentro a los vértices: Los vectores que van del baricentro G a los vértices del triángulo ABC tienen como suma el vector nulo.
Demostración
Como se sabe, $3G=A+B+C$. De aquí que $0=A-G+B-G+C-G=GA+GB+GC$.
Fórmula de Sylvester: Los vectores que van del circuncentro O a los vértices del triángulo ABC tienen como suma al vector que va del circuncentro O al ortocentro H.
Demostración
Sea $H$ el punto que cumple la ecuación vectorial $OA+OB+OC=OH$. Vamos a demostrar que $H$ pertenece a las tres alturas del triángulo $ABC$.
Para ello, sean $L,M,N$ los puntos medios de los lados $BC,CA, AB$, respectivamente. Entonces, recordando que un isósceles es la mitad de un rombo, se tiene
$OA+OB+OC= OH$ si y sólo si $OA+2OL=OH$, si y sólo si $2OL=AO+OH=AH$. Lo cual significa que $H$ está en la altura de $A$ respecto a $BC$. De manera similar se logran las otras dos conclusiones (las incluyo):
$OA+OB+OC= OH$ si y sólo si $OB+2OM=OH$ si y sólo si $2OM=BO+OH=BH$. Lo cual significa que $H$ está en la altura de $B$ respecto a $CA$.
$OA+OB+OC= OH$ si y sólo si $2ON+OC=OH$ si y sólo si $2ON=CO+OH=CH$. Lo cual significa que $H$ está en la altura de $C$ respecto a $AB$.
Recta de euler: Los tres puntos notables del triángulo, circuncentro O, baricentro G y ortocentro H, se encuentran sobre una misma recta.
Demostración (puramente vectorial)
Como se sabe, $GA+GB+GC=0$. Pero esta ecuación vectorial es equivalente a esta otra: $GO+OA+GO+OB+GO+OC=0$. Es decir, a $3GO+OA+OB+OC=0$.
Pero acabamos de aprender la fórmula de Sylvester. Por tanto, $3GO+OH=0$. Es decir, $3OG=OH$. Es decir, O,G y H son colineales. (Y se puede decir más: ...se deja como ejercicio para el lector.)
Los saluda
jmd
