Blogs
Identidad notabilísima --y su determinante
Me he encontrado en estos días con la notabilísima identidad algebraica (para a,b,c reales):
$$abc+(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)$$
Su rasgo distintivo radica --creo-- en que el lado derecho refleja el izquierdo pero intercambiando la suma por el producto y éste por aquélla. Es decir, lo que en el lado izquierdo es producto en el derecho es suma y la suma en el izquierdo es producto en el derecho.
Seguir la regla y "ver como" en álgebra
Ahora que el 2014 se ha quedado atrás y el puente Guadalupe Reyes se terminó es buen momento para mirar hacia el futuro. Y desearle a toda la comunidad de usuarios de MaTeTaM un 2015 de eficaces aprendizajes en el problem solving de matemáticas.
Y, bueno, de paso voy a plantear la tesis de que, en el aprendizaje de las matemáticas, primero se aprende el procedimiento y sólo después de ello se aprende el concepto. Ilustro con un ejemplo de desigualdades.

Riesgo moral y agencia --en educación superior
En este fin de 2014 en que la Academia de Ciencias sueca otorgó el premio Nobel de economía a Jean Tirole, puede que sea de alguna utilidad comentar sobre su enfoque (la Teoría de la Agencia) al analizar los mercados y su regulación. (Añado una discusión sobre la situación de la educación superior vista desde la perspectiva de esta importante teoría.)

Desigualdad de Titu --una demostración booteable
Voy a presentar en este post una forma de demostrar la desigualdad de Titu Andreescu que recuerda los procesos de bootstraping utilizados en computación --y otras áreas de la ciencia. El término bootstrapping está inspirado --verosímilmente-- en Las Sorprendentes Aventuras del Baron de Munchausen. (Una serie de narraciones donde el héroe realiza tareas imposibles.) Atacho una traducción al español.

Examen de la XXVIII OMM. Segundo día.
A continuación el examen del segundo día de la XVIII Olimpiada Mexicana de Matemáticas que se está aplicando a los concursantes el día de hoy en Toluca.
Problema 4 de la XXVIII OMM Segundo Día. Toluca 2014
Problema 5 de la XXVIII OMM Segundo Día. Toluca 2014
Problema 6 de la XXVIII OMM Segundo Día. Toluca 2014
Sobre el problema 3 del selectivo final
El problema y la solución de Germán
Cuadrilátero cíclico: más instancias de uso
En este post voy a recomendar el estudio de algunos materiales sobre cuadriláteros cíclicos a quienes se están preparando para el nacional. De paso intercalo dos instancias de su uso.
En un post anterior --dedicado a los criterios de reconocimiento de los cuadriláteros cíclicos-- hemos destacado la importancia de esta herramienta en el problem solving de geometría y discutimos varias instancias de uso asociadas a demostraciones del teorema de la mariposa.
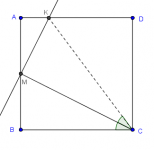
Selectivo 2 OMM_Tam_2014
Enseguida presento los cuatro problemas del segundo examen selectivo para la preselección Tamaulipas OMM 2014. Añado las soluciones al 2 y al 4.
Problema 1. En un cuadrilátero ABCD convexo se trazan las perpendiculares desde cada vértice a la diagonal que no pasa por él. Demostrar que los cuatro puntos de intersección de cada perpendicular con su correspondiente diagonal forman un cuadrilátero semejante al dado.
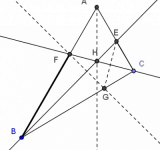
Primos y divisibilidad: dos problemas
Voy a comentar en este post las soluciones de los problemas 1 y 2 del primer selectivo para la preselección OMM Tamaulipas 2014. Espero que sirva como feedback para los preseleccionados que no los resolvieron o los resolvieron de otra forma. (Vaya una felicitación para Camilo por su excelente elección de los problemas.)
Problema 1. Sean m,n enteros positivos tales que $m^2+n^2$ es múltiplo de 3. Pruebe que m y n son también múltiplos de 3.
Comentario:
