Blogs
Cuadrilátero cíclico --criterios e instancias de uso
Puesto que el material disponible en la Web sobre los cuadriláteros cíclicos no incluye las demostraciones de los criterios de su reconocimiento (con excepciones difíciles de encontrar) voy a presentar en este post los tres criterios para el reconocimiento de un cuadrilátero cíclico, así como sus demostraciones. Añado tres instancias de uso.
Definición y criterios de reconocimiento
Primero la definición:
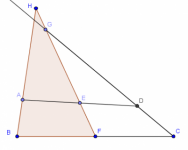
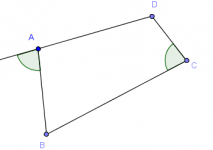
Si los cuatro vértices de un cuadrilátero convexo están sobre la misma circunferencia, entonces se dice que el cuadrilátero es cíclico.
Pensamiento lateral (¡¿Alguien me puede explicar eso?!)
Me he encontrado en estos días con el tema del pensamiento lateral y, sobre todo, con sus acertijos. Y creo que puede ser de alguna utilidad para los lectores de MaTeTaM una discusión sobre esos acertijos y su relación con los chistes y los problemas de matemáticas de concurso. La clave que los une es la interpretación de unos datos desde un cierto punto de vista.
El difícil de la ONMAPS --Tamaulipas 2014
Concurso Municipal OMM Tamaulipas 2014
Hoy 4 de abril de 2014 se aplicó el examen del concurso municipal, primera etapa del proceso de selección de la Olimpíada Mexicana de Matemáticas en Tamaulipas. Pongo en este post los problemas con sus soluciones (algo condensadas) como una retroalimentación para los participantes.
1. En un examen de 10 preguntas, Juan las respondió todas y obtuvo 29 puntos. Si le dieron 5 puntos por cada respuesta correcta y -2 por cada incorrecta ¿cuántas preguntas respondió Juan correctamente?
Solución
El modelo algebraico es: x+y=10, 5x-2y=29. La respuesta es x=7.
El difícil de la olimpiada de la SET (Jugando con las Matemáticas)
Ocho albañiles construyen una barda de 30 metros en 9 días trabajando 6 horas diarias. ¿Cuántos días tardarán 10 obreros para construir 50 metros de barda trabajando 8 horas diarias?
Este problema fue el último (el 5) del examen estatal de la olimpiada para tercero de secundaria celebrada el 26 de marzo en Cd Victoria Tamaulipas. Ninguno de los tres concursantes lo resolvió. ¿En qué consiste su dificultad? Voy a comentar en este post la solución y a compararlo con un problema clásico de proporcionalidad inversa.
Reflexiones sobre un curso en Jaumave
Tomando como pretexto un curso en resolución de problemas que impartí el sábado en Jaumave, voy a comentar en este post sobre la forma en que los profesores de primaria ven los nuevos contenidos de matemáticas en quinto y sexto grados y su actitud ante algunos de los problemas de las guías del maestro.
Elegí uno de esos problemas para comentar sus implicaciones y su razón de ser desde un punto de vista didáctico. Finalizo enunciando 10 acertijos clásicos (los cuales se comentarán después --en un nuevo post o como postdata a éste).
¡Tienes que ver la conexión!
En este post voy a comentar sobre una estrategia del problem solving de concurso que podríamos llamar ¡Tienes que ver la conexión!. Lo haré a través de dos ejemplos clásicos y relativamente bien conocidos en los círculos de la olimpiada de matemáticas.
Problema 1: Si la suma de dos números es 2 y su producto es 3 ¿cuál es la suma de sus recíprocos?
Brilliant: un sitio Web para el talento matemático juvenil
En estos días de febrero Valentina y Jesús vinieron a Cd. Victoria de visita y me recomendaron visitara y navegara el sitio Web https://brilliant.org/, un sitio extraordinariamente bien construido y con los mismos temas de MaTeTaM. La idea sería decidir si matetam.com pudiera aspirar a brilliant.org --o, por lo menos, adoptar su formato.
Enseguida describo mi experiencia en brilliant y, al mismo tiempo, extiendo con ello una invitación a los usuarios de matetam.com para que visiten brilliant y pongan manos a la obra en el problem solving de concurso.
La caja de Arquímedes: un rompecabezas milenario

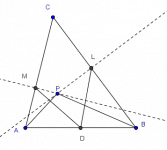
Soluciones múltiples para un problema geométrico
Una vez superada la cuesta de enero encontré este problema de geometría en la Web el cual comparto con los lectores de MaTeTaM. Doy la solución vectorial y varias sugerencias para soluciones sintéticas. (La idea es recomendar a los cognizadores preparándose para concursos de matemáticas escolares a no abandonar un problema después de obtener una solución. Buscar otras soluciones los hará más sabios en el arte del problem solving.)