Blogs
El 5 del VI concurso nacional OMM 1992
Cuando llueve, como en estos días que se formó en el Golfo de México la tormenta Ingrid, me pongo inspirado y con ganas de postear. Buscando qué hacer mientras llovía me encontré con este problema del concurso nacional de 1992 (VI OMM).
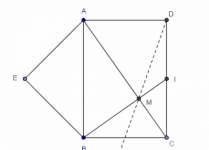
Teorema fundamental de la proporcionalidad (Tales)
Si una recta paralela al lado $BC$ del triángulo $ABC$ corta en $B'$ a $AB$ y en $C'$ a $AC$), entonces $$\frac{AB}{AB'}=\frac{AC}{AC'}=\frac{BC}{B'C'}$$
Este es el Teorema de Tales para triángulos del cual hemos hablado ya en MaTeTaM. En esta oportunidad comentaré el teorema particularizado para triángulos rectángulos y lo demostraré con el método de áreas.
Método Singapur --para razonar problemas verbales elementales
Llamo problemas verbales (word problems) a los problemas razonados con los que se introduce (o debería introducirse) el razonamiento matemático en la escuela primaria (en quinto y sexto año por lo menos). Voy a ilustrar el tema con
Un ejemplo
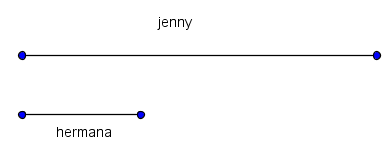
Jenny tiene 7 pesos y su hermana 2. Después de que su madre les da una misma cantidad de pesos Jenny tiene el doble que su hermana. ¿Cuánto recibieron de su madre?
Solución algebraica
El fácil del concurso XV OMM (2001)
Con motivo del comentario-solución de Germán Puga Castillo al problema 1 del concurso nacional de la OMM 2001 (y el feedback de Jesús Rodríguez Viorato), el problema llamó mi atención por su aparente simplicidad. Voy a comentarlo en este post (y a resolverlo apoyándome en la idea de Germán). El problema es el siguiente:
Encuentra todos los números de 7 dígitos que son múltiplos de 3 y de 7, y cada uno de cuyos dígitos es 3 o 7.
Dos problemas razonados --para segundo de secundaria
En este post voy a discutir dos problemas razonados que, según la reforma de secundarias 2011, los alumnos que pasan a tercer año deberían estar en posibilidad de resolverlos. Su modelación conduce a un sistema $2\times2$ (dos ecuaciones, dos incógnitas).
Idealmente están al alcance de un adolescente de 14, pues en el bloque V del programa de matemáticas de segundo de secundaria, uno de los aprendizajes esperados es:
Resuelve problemas que implican el uso de sistemas de dos ecuaciones lineales con dos incógnitas.
Análisis de algunos problemas ENLACE 2012
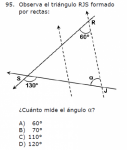
Cuatro problemas elementales de aritmética
En los entrenamientos de la selección ONMAS Tamaulipas 2013 me tocaron 2 sesiones de 3 horas cada una. De ahí elegí 4 problemas de aritmética para presentarlos en este post, en el cual voy a resolverlos y a comentarlos.
A pesar de ser elementales, están lejos de ser triviales. Digo, considerando que fueron para alumnos de primaria y secundaria. (Para el alumno promedio muy probablemente cada uno de ellos es un proyecto de investigación.)
La profecía de la húngara --y Freud
En este post voy a comentar un caso de inconformidad de la mamá de un niño de Tampico sobre la supuesta injusticia cometida contra su hijo. Lo hago poniendo como telón de fondo un chiste de Sigmund Freud.
El tema me parece importante para la organización de los concursos en Tamaulipas pues se debería evitar la intervención de las mamás en la organización de ellos (eso creo). El caso me recordó otro similar en 2009, el cual motivó mi renuncia como delegado Tamaulipas de la OMM.
ONMAS Tamaulipas 2013: los problemas y algunas soluciones
En este post voy a presentar los problemas del concurso ONMAS Tamaulipas 2013 y a comentar algunos de ellos.
Los problemas
Concurso Estatal ONMAS Tamaulipas 2013; UAMCEH-UAT, Cd. Victoria, 19 de abril (Cada problema 7 puntos, no se permiten calculadoras ni celulares. Duración: 4 hrs
1N. Encontrar todos los enteros positivos n tales que 3n+4 es múltiplo de 5.
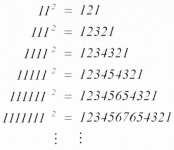
Quinta lección: Resolución de problemas
En este post final del curso de resolución de problemas voy a presentar 23 problemas. La solución o sugerencia se pondrá en otro post adicionada con comentarios.
Los problemas se etiquetan con A si de álgebra, con C si de combinatoria, con G si de geometría y con N si son de números. La mayoría de los problemas son elementales pero se buscó que fueran interesantes.
1N. El abuelo reparte 500 pesos entre sus 18 nietos de manera que cada nieta reciba 2 pesos menos que cada nieto. ¿Cuántas nietas tiene y cuánto les tocó en el reparto?

