Básico
Multiplica las fechas
En una fecha escrita de la forma aa/mm/yy o a/m/yy se multiplican los digitos usados para escribirlas, por ejemplo 24/12/22 da 2x4x1x2x2x2=64 o 5/8/22 da 5x8x2x2=160. ¿Cuántas fechas de la década de los 2020's cumplen que la multiplicación de los dígitos da 120?
Suelo con mosaicos
Un suelo se va a llenar con mosaicos como el siguiente, formado por mosaicos cafés más pequeños como los mostrados en la figura. El área blanca se llenará con mosaicos azules del mismo tamaño que el café. Al llenarse todo el suelo se utilizaron 192 cafés, ¿cuántos mosaicos azules fueron necesarios?

Piezas rectangulares con área 240
Se van a construir piezas rectangulares de área 240 cm2 y con ambos lados entero. ¿De cuántas formas distintas se puede hacer?
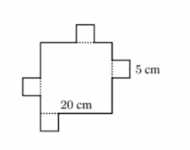
Halla el perímetro
Sobre los lados de un cuadrado de 20 x 20 cm se dibujan cuadrados de 5 x 5 cm como se muestra en la figura. ¿Cuál es el perímetro de la siguiente figura?
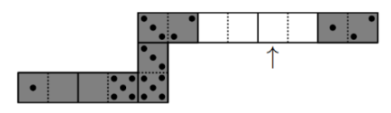
Fichas de dominó
Pancho hizo una hilera con 7 fichas de dominó de manera que los lados con el mismo número de puntos quedaron uno al lado del otro. Originalmente la hilera tenía un total de 33 puntos, pero el hermanito de Pancho se llevó dos de las fichas. ¿Qué cantidad de puntos había en el lugar que señala la flecha en la figura?
Demostrar que es equilatero
Sea ABCD un cuadrado.
Se construyen 2 triangulos equilatero hacia afuera, CDE y BCF, se trazan las circunferencia con centro en E y con Centro en F que pasan por CD y BC respectivamente.
Sea P la interseccion de las circunferencias.
Demuestra que el trianguo PDB es equilatero.
Parejas Guerreras
Una pareja de enteros positivos $m,n$ es guerrera si existen enteros positivos $a,b,c,d$ con $m=ab, n=cd$ y $a+b=c+d$. Por ejemplo, la pareja 8,9 es guerrera pues $8 = 4 \cdot 2 , 9=3 \cdot 3$ y $4+2=3+3$. Se colorean los enteros positivos de la siguiente manera:
- Empezamos coloreando el 3 y el 5.
- Después , si algún entero positivo no está coloreado y este tiene una pareja guerrera que ya está coloreado, entonces lo coloreamos.
Encuentra todos los enteros positivos que eventualmente se colorean.
Circunferencias con relación de radios
Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ dos circunferencias tangentes externamente en $S$ tales que el radio de $\mathcal{C}_2$ es el triple del radio de $\mathcal{C}_1$. Sea $l$ una recta que es tangente a $\mathcal{C}_1$ en $P$ y tangente a $\mathcal{C}_2$ en $Q$, con $P$ y $Q$ distintos de $S$. Sea $T$ el punto en $\mathcal{C}_2$ tal que $TQ$ es diámetro de $\mathcal{C}_2$ y sea $R$ la intersección de la bisectriz de $\angle SQT$ con el segmento $ST$. Demuestra que $QR = RT$
Cíclico dentro de un isóceles
Sea $ABC$ un triángulo con $AB=AC$ de gravicentro $G$. $M$ y $N$ los puntos medios de $AB$ y $AC$ respectivamente y $O$ el circuncentro del trángulo $BCN$. Muestra que $MBOG$ es un cuadrilátero cíclico.
Suma de cubos igual a 2016
Determina si existen alguna terna de enteros no negativos, no necesariamente distintos, $(a,b,c)$ tales que:
$$a^3 + b^3 + c^3 =2016$$
