Álgebra

Los problemas y ejercicios que a continuación presento son de ecuaciones cuadráticas, quizá uno de los temas más avanzados de las matemáticas escolares. Ello supone que el alumno ya domina los temas más básicos asociados con la suma, resta y multiplicación de expresiones algebraicas --y las instancias de uso de la regla distributiva. 

Problemas cuadráticos: completar el trinomio

El método de completar el trinomio cuadrado perfecto se puede usar para resolver ecuaciones cuadráticas. Presento enseguida un ejemplo y varios ejercicios.

Consideremos la siguiente ecuación cuadrática: $x^2+10x=39$.

En el mes de noviembre pasado en México se le armó un escandalito al diputado Arellano por tratar de adornar su discurso con un refrán popular: "la tierra es como las mujeres, hay que trabajarla y abonarla" (http://www.proceso.com.mx/?p=324460).

Algunas diputadas consideraron ofensivo que se viera a la mujer como productora de niños y Arellano tuvo que disculparse y solicitar que se borrara esa frase de la minuta.

En este post voy a comentar sobre el método de reagrupamiento para factorizar una ecuación cuadrática y su correspondiente solución diagramática. Ilustro con un caso particular de toda

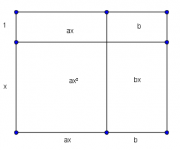
Una familia de problemas cuadráticos

En una ecuación cuadrática, si se puede factorizar entonces se puede representar como rectángulo --con uno de sus factores la base y el otro la altura.

Consideremos el problema de factorizar la ecuación cuadrática
$$ax^2+(a+b)x+b=0$$
(donde $a,b$ son enteros positivos).

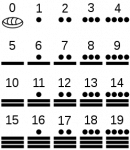
Los sistemas de numeración son símbolos y reglas para denotar cantidades  Muchas civilizaciones inventaron los suyos, por ejemplo, los romanos usaron la notación I, II, III, IV, .. etcétera.

En nuestros tiempos, el sistema de numeración que usamos cotidianamente se llama sistema de numeración posicional en base 10 (o simplemente sistema decimal).  Es decimal pues se usan diez símbolos (a saber  0, 1, 2, 3, 4, 5, 6, 7, 8, 9) y depende de la posición pues no es lo mismo 12 (uno dos) que 21 (dos uno).

En el siguiente post voy a comentar algunas leyes de Murphy relacionadas con la pregunta 92 de ENLACE 2012 (3o Sec.), la cual es de plano una metida de pata extrema de los diseñadores de las preguntas.

Si dos cantidades son iguales entonces son intercambiables --en el cálculo o demostración.

Parece trivial. Y lo es. Pero hay que aprender a usarlo. Antiguamente se solía decir:

Dos cosas iguales a una tercera son iguales entre sí.

Pero no se trata de aprender a recitarlo, se trata de aprender a usarlo.

Ejemplos:

1. Considere el sistema $x+y=z$, $z=5$

Aquí tenemos que (dos cosas) $x+y$ y 5 son iguales a $z$ (una tercera).  Por tanto, $x+y=5$ (son iguales entre sí).

En este post voy a presentar el conocido procedimiento de dividir un polinomio entre $x-c$ denominado división sintética.

División larga en polinomios

Consideremos la fracción racional $$\frac{x^3-2x^2-x+2}{x-1}$$ Y supongamos que deseamos efectuar la división con miras a simplificarla.

Ante algunas conductas de mis alumnos para las cuales no sé cómo reaccionar, he estado tentado más de una vez a saltar hacia atrás como Condorito o, mínimo, exclamar ¡PLOP! (la de ¡Exijo una explicación! es menos adecuada --creo).

Les cuento (la materia es antropología de la educación):

 En este post voy a presentar la cuestión de que si el alumno no cumple los pre-requisitos para estar en un cierto nivel escolar, entonces la educación se convierte en una farsa. Porque, siendo realistas, el profesor no tomará medidas remediales para sus alumnos más débiles. En primer lugar porque el tiempo del aula es un recurso escaso. En segundo lugar porque interpretará los excesivamente laxos filtros de entrada  de la administración escolar como un insulto a su profesión. (Un primer pre-requisito es ¿sabe leer? --¿es esto mucho pedir?).

 Voy a comentar en este post la tesis de que, si el estudiante va a independizarse tarde o temprano de la escuela y continuar con su aprendizaje de manera autodidacta, lo mejor es que aprenda a leer libros. ("¿Quieres decir que los estudiantes no saben leer? No. Lo que quiero decir es que los libros siguen un cierto estilo de escritura con el cual hay que familiarizarse.") Ilustro la tesis con la redacción clásica de una solución a un problema. Y se empieza a aplicar un método de lectura que ha probado su eficacia en la práctica.