Geometría
IMO 2012 --los problemas de geometría
En los problemas de la IMO, la dificultad para un aficionado a las matemáticas de concurso (como el que esto escribe) no es el resolverlos (esa es casi una imposibilidad) sino el entender las soluciones publicadas. Voy a comentar en este post las soluciones de los problemas 1 y 5 de la 53 International Mathematical Olympiad (2012) que se celebró en Mar del Plata (Argentina) del 4 al 16 de julio.
Para el problema 1 me faltaba un teorema, para el 5 el plan de solución. Es decir, para el 5 la solución publicada la podía seguir, pero me quedaba la incógnita de por qué o cómo esa ruta de solución era la correcta o por qué.

El misterioso hechizo del problem solving
En días pasados subí a MaTeTaM todos los problemas de la ONMAS que pude encontrar, y hubo uno que ya había publicado en 2010 y que llamó mi atención pues se ve bastante difícil... y más difícil es la solución que envió Brandon en su momento (basada en una semejanza).
Bueno, lo difícil es entender la demostración que da de la semejanza --yo no le entendí. El caso es que lo traje en al cabeza varios días, lo resolví de otra manera (por ortocentro) y generé un problema parecido... pero no podía demostrar la semejanza (que parecía obvia en la figura) de una manera alternativa a la que dio Brandon.
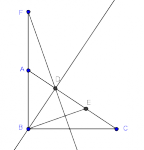
Discusión sobre las coordenadas de un punto
Teorema de la altura: una prueba visual
En nuestra sociedad globalizada, en la que el espectáculo y la diversión han sido puestos en el centro por los mass media, es muy difícil ser profesor, de cualquier cosa, pero sobre todo de matemáticas. ¿Tiene que ser convertida el aula en un reality show para atraer la atención de nuestros estudiantes?
Problemas del primer selectivo OMM_Tam_2011
En este post presento los 7 problemas del primer selectivo aplicado a la preselección Tamaulipas OMM 2011 y se añaden sugerencias para sus soluciones. Los problemas son elementales y no deberían presentar mayores dificultades para al menos la mitad de los preseleccionados.
Introducción
Atendiendo una invitación de Ramón Llanos, el primer entrenamiento de la preselección Tamaulipas de la Olimpiada Mexicana de Matemáticas, Delegación Tamaulipas, estuvo a mi cargo.
En ese entrenamiento pude concretizar la propuesta de entrenamiento hecha en el post anterior denominado El difícil del estatal
El difícil del estatal (OMM_Tam_2011)
El Cuadrado de Sócrates --y los triángulos notables
Voy a discutir en este post cuatro problemas de geometría básica que se resuelven de manera elemental invocando dos triángulos notables. Estos triángulos son el isósceles rectángulo (la mitad de un cuadrado) y el 30-60-90 (la mitad de un triángulo equilátero). En los dos problemas de inicio, la solución presentada invoca el isósceles rectángulo; en los otros dos se debe invocar la mitad de un equilátero.
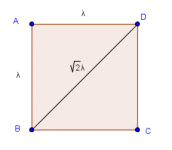
Primer problema (el Cuadrado de Sócrates)
Dado el lado $\lambda$ de un cuadrado, construir el cuadrado del doble de área.
Solución
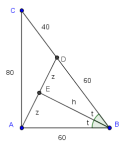
Sobre la utilidad de saber trigonometría
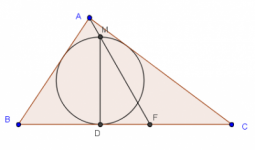
Discusión sobre incírculos y excírculos
Voy a discutir en este post algunos conceptos relacionados con las circunferencias incrita y exinscrita. Dichos conceptos forman un todo y conviene aprenderlos en paquete --es muchísimo más fácil retenerlos en la memoria y comprenderlos si se aprenden en sus interconexiones.
Se trata de los conceptos de semiperímetro --en el contexto de ciertas simetrías entre las longitudes de las tangentes de circuncírculo y excírculos--, el concepto de puntos isotómicos, y el de los puntos de Gergonne y Nagel --como ejemplo de puntos conjugados isotómicos.
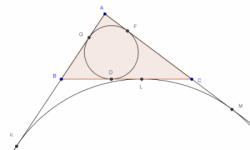
Un problema clásico de homotecia
Durante el año 2009, al final de uno de los entrenamientos de la OMM Delegación Tamaulipas, Jesús Rodríguez Viorato le planteó el siguiente problema a Luis Brandon --el líder de la selección 2009:
El incírculo de un triángulo $ABC$, es tangente en $D$ al lado $BC$ y $DM$ es un diámetro. El rayo $AM$ corta en $F$ el lado $BC$. Demostrar que $BD=CF$.