Problemas - Álgebra
Coeficientes de una expresión cuártica
Calcular el valor de la expresión $(a_0+a_2+a_4)^2-(a_1+a_3)^2$, donde los $a_i$ son los coeficientes de la expansión de $(2x+\sqrt{3})^4$: $$(2x+\sqrt{3})^4=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4$$
Desigualdad de Jensen
Sea $f:\mathbb{R} \to \mathbb{R}$ una función punto medio convexa, es decir, que satisface que: $$f\left( \frac{x+y}{2} \right) \leq \frac{f(x)+f(y)}{2} $$ para toda pareja de números reales $x,y \in \mathbb{R}$.
Demostrar que para cualesquiera números reales $a_1, a_2, \ldots, a_n$ se satisface la siguiente desigualdad: $$f \left(\frac{a_1+a_2+ \cdots +a_n}{n} \right) \leq \frac{f(a_1)+f(a_2)+\cdots +f(a_n)}{n}.$$
Composición de la función "suma de sus dígitos"
Para un entero positivo $ n $ se definen $n_1$ como la suma de los dígitos de $ n $, $n_2$ como la suma de los dígitos de $n_1$, y $n_3$ como la suma de los dígitos de $n_2$.
Por ejemplo para $n = 199$, $n_1 = 199_1 = 19, n_2 = 199_2 = 10$ y $n_3 = 199_3 = 1$.
Encuentra todas las parejas de enteros positivos $(m, n)$ tales que:$$m + n = 2007$$ $$m_3 + n_3 = 2007_3$$
Desigualdad homogenea
Sean $a, b, c$ números reales positivos que satisfacen $a+b+c = 1$.
Muestra que: $$\sqrt{a + bc} + \sqrt{b + ca} + \sqrt{c + ab}\leq 2.$$
Juego de caballeros
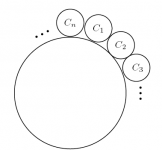
Los caballeros $C_1,C_2,\ldots,C_n$, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:
El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con $C_1$, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.
P6 OMM 2006. Problema con números surtidos
Sea $n$ la suma de los dígitos de un entero positivo $A$. Decimos que $A$ es “surtido” si cada uno de los enteros $1,2,\ldots,n$ es suma de dígitos de $A$
- Demuestra que si $1,2,\ldots,8$ son sumas de dígitos de un entero $A$ entonces $A$ es surtido.
- Si $1,2,\ldots,7$ son sumas de dígitos de un entero $A$, ¿es $A$ necesariamente surtido?
Nota: El número 117 no es surtido pues sólo $1=1, 2 = 1+1, 7 = 7, 8 = 1 + 7, 9 = 1 + 1 + 7$ se pueden escribir como suma de dígitos de 117.
P4 OMM 2005. Eliminar (ternas aritméticas) reordenando
Decimos que una lista de números $a_1,a_2,\ldots,a_m$ contiene una terna aritmética $a_i,a_j,a_k$, si $i<j< k$ y $2a_j = a_i + a_k$. Por ejemplo, 8,1,5,2,7 tiene una terna aritmética (8,5 y 2) pero 8,1,2,5,7 no. Sea $ n $ un entero positivo. Muestra que los números $1,2,\ldots,n$ se pueden reordenar en una lista que no contenga ternas aritméticas.
P2 OMM 2005. Matrices n-balanceadas
Dadas varias cuadrículas del mismo tamaño con números escritos en sus casillas, su suma se efectúa casilla por casilla. Por ejemplo:
Dado un entero positivo $N$, diremos que una cuadrícula es $N$-balanceada si tiene números enteros escritos en sus casillas y si la diferencia entre los números escritos en cualesquiera dos casillas que comparten un lado es menor o igual que $N$.

P2 OMM 2004. Diferencia no menor que el centésimo del producto
¿Cuál es la mayor cantidad de enteros positivos que se pueden encontrar de
manera que cualesquiera dos de ellos $a$ y $b$ (con a $a\neq b$) cumplan $|a-b|\geq{\frac{ab}{100}$?
Problema 6, IMO 2010
Sea $a_1, a_2, a_3, \ldots$ una sucesión de números reales positivos. Se tiene que para algún entero positivo $s$,
$$a_n = \textrm{max}\{a_k + a_{n-k} \textrm{ tal que } 1 \leq k \leq n - 1\}$$
para todo $n > s$. Demuestre que existen enteros positivos $\ell$ y $N$, con $\ell \leq s$, tales que $a_n = a_\ell + a_{n-\ell}$ para todo $n \geq N$.
