Problemas - Combinatoria
Problema 5
Cuantos números de 3 cifras, que la suma de sus cifras sea par se pueden formar con los digitos 1,2,3...9
Famosas decadentes adictas al bisturí
En una muestra de 50 famosas, 35 han recurrido a la mamoplastia, 20 a la rinoplastia y 15 a la liposucción. Se logró averiguar también que 15 se habían practicado mamo y rinoplastia, 12 rinoplastia y liposucción, y 10 liposucción y mamoplastia. Se supo adicionalmente que 8 se habían sometido a las tres intervenciones estéticas.
Diagrama de Lewis Carroll: instancia de uso en conteo
Ingresaron 100 estudiantes a la facultad. De ellos, 40 son del sexo femenino, 73 eligieron la licenciatura en Comunicación Multimedia, y 12 del sexo femenino no eligieron Comunicación Multimedia. ¿Cuántos estudiantes de esos 100 son del sexo masculino y no eligieron Comunicación Multimedia?
Modelación recursiva
¿De cuántas formas se puede formar un número con los dígitos 1 y 2 (y ningún otro) de tal manera que sus dígitos sumen n?
XXIIIOMM Problema 6
En una fiesta con n personas se sabe que de entre cualesquiera 4 personas, hay 3 de las 4 que se conocen entre sí o hay 3 que no se conocen entre sí. Muestra que las n personas se pueden separar en 2 salones de manera que en un salón todos se conocen entre sí y en el otro salón no hay dos personas que se conozcan entre sí.
XXIIIOMM Problema 2
En cajas marcadas con los números 0,1,2,3,... se van a colocar todos los enteros positivos de acuerdo con las siguientes reglas:
Contar clasificando
¿Cuántos triángulos hay en la figura?
Eliminación con dos operaciones
En cada cuadrado de un tablero rectangular hay un entero positivo. Se pueden modificar los números del tablero usando alguno de los siguientes movimientos.
--Multiplicar por 2 cada número de un renglón.
--Restar 1 a cada número de una columna.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 6)
Alrededor de una circunferencia se marcan 6000 puntos y cada uno se colorea con uno de 10 colores dados, de manera tal que entre cualesquiera 100 puntos consecutivos siempre figuran los 10 colores. Hallar el menor valor k con la siguiente propiedad: Para toda coloración de este tipo existen $k $ puntos consecutivos entre los cuales figuran los 10 colores.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 1)
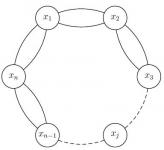
Sea $ n $ un natural mayor que 2. Supongamos que $ n $ islas están ubicadas en un círculo y que entre cada dos islas vecinas hay dos puentes como en la figura: