Es un lugar común el decir "cuestión de enfoques" o "según el cristal con que se mira", etc. Si bien todas esas frases están orientados al optimismo, mejor dicho, a lograr el optimismo de terceros, es también cierto que la perspectiva que se adopte para mirar un problema es clave para su comprensión y, en consecuencia, la acción eficaz para resolverlo.
Decir "medio lleno o medio vacío" no aporta absolutamente nada a la cognición de un estado de cosas. A menos que ese estado de cosas se vea desde la perspectiva de un proceso: 1) si lo estoy llenando y el llenado es costoso, entonces, al decir que solamente falta la mitad de llenar, estamos adoptando una forma de ver el estado de cosas de manera optimista; pero 2) si se está vaciando y ya va a la mitad y el líquido derramado es valioso, lo que se tiene que hacer es parar el vaciado (de alguna manera y si se puede) y de nada nos sirve que lo veamos como medio lleno.
Por otro lado, la frase "nada es verdad ni mentira, todo depende del cristal con que se mira" tampoco está orientada a la cognición sino que asume una perspectiva relativista para mirar el mundo. Y, sin embargo, la metáfora del cristal ya está más cerca de un uso en solución de problemas. (El cristal representaría la perspectiva adoptada para mirar el problema.)
Para ilustrar el poder de una perspectiva (de un framing) , de una forma de ver un problema, consideremos el problema 2 de la IMO 2009:
Sean ABC un triángulo de circuncentro O, P y Q puntos sobre AB y AC, respectivamente, y K, L, M los puntos medios de BQ, CP y PQ, respectivamente. Si el circuncírculo del triángulo KLM es tangente a PQ, demostrar que OP=OQ.
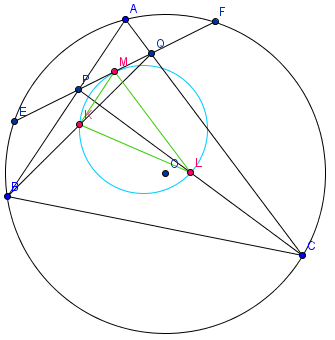
Aquí el problema planteado es probar isósceles. Y ¿cómo se demuestra isósceles? Bueno, hay varias formas: ángulos en la base iguales, la mediana es mediatriz (la estrategia usada por Brandon), la bisectriz es mediana, etc. Pero hay una que es poco usada y es trivial pero que en este problema es muy valiosa y, se puede decir, ilumina todo el problema (las gracias le sean dadas a JRV por llamar mi atención hacia esa estrategia de probar isósceles).
Se trata de una propiedad trivial de la potencia de un punto: OP=OQ si y sólo si P y Q tienen la misma potencia respecto a un círculo cualquiera centrado en O. Y en este problema, de acuerdo a esa estrategia, lo que se tiene que probar es $PA\cdot PB=QA\cdot QC$. (Como se sabe --o se debería saber-- el problema debe salir con los datos en el enunciado e interpretados y exprimidos en sus consecuencias hasta que ya no quede más nada que exprimir. Es decir, se tienen que aprovechar los puntos y líneas de la configuración geométrica a que da lugar el enunciado.)
¿Por qué esta perspectiva es valiosa? Bueno porque proporciona una meta muy concreta a lograr y aparentemente factible. Y ello conduce al cognizador a adoptar una lógica de necesidades. Es decir, la meta misma le dice cuál es la información concreta que debe buscar en la configuración y en el enunciado.
Comparemos con una análisis exploratorio sin ninguna idea concreta sobre cómo vamos a probar isósceles. De entrada, es fácil ver dos pares de paralelas: KM//PB y ML//QC (ambos resultados por el teorema de la línea media --segmento por puntos medios de dos lados es paralelo a la base y mide la mitad de ésta). Y se puede decir más: PB=2KM y QC=2LM. Después seguiría una cacería de ángulos aprovechando esos pares de paralelas y los ángulos inscritos. Pero el análisis exploratorio aquí se detiene porque no se ve nada más que se pueda hacer y el cognizador debe regresar a la pregunta clave: ¿cómo probar isósceles?
Se espera que el cognizador aguerrido descubra tarde o temprano alguna forma de probar OP=OQ. (Sería mejor temprano que tarde.) A Brandon se le ocurrió la estrategia de probar que la mediana OM es también mediatriz, posiblemente mediante la asociación de ideas a que da lugar que M es punto medio de PQ. Esto lo condujo a lograr la submeta de probar M punto medio de la cuerda que contiene PQ (con lo cual ya estaría el problema resuelto pues radio por el punto medio de la cuerda es perpendicular a la cuerda).
Notemos que la estrategia de Brandon queda sugerida después de pensar en OP=OQ como "P y Q equidistantes del centro O" ¿Cómo? ¡Porque O es el centro de un círculo! Y esto lleva a "radio y cuerda perpendiculares" (Es decir, si no se ve O como centro no hay asociación de ideas hacia la cuerda y el radio.) Sin embargo, me queda la duda de cómo llegó Brandon a ver la semejanza APQ~MLK.
Pero volvamos a la estrategia de la potencia de P y Q, y la lógica de necesidades que genera. Como decíamos antes, de acuerdo a esa estrategia, lo que se tiene que probar es $PA\cdot PB=QA\cdot QC$. Y esto sugiere, al poner la igualdad como la proporción $PA/AQ=QC/PB$, buscar una semejanza entre el triángulo APQ y algún otro (porque QC y PB no son lados de ningún triángulo). Y aquí es donde entra el análisis exploratorio iniciado al principio.
Porque QC=2LM y PB=2KM. Y ya está. Porque entonces la proporción a que da lugar la ecuación de potencias inicial se convierte en $PA/AQ=QC/PB=KM/LM$. Es decir, tenemos de aquí la submeta de demostrar la semejanza APQ~MLK. (Notemos que lograr ver QC=2LM y PB=2KM puede tardar en llegar, pero la confianza en que la estrategia es la correcta --aquí es donde entran los afectos a ayudar a la cognición-- debería hacer que el cognizador persista y no abandone sólo al ver que QC y PB no son lados de ningún triángulo.)
Para lograr la semejanza APQ~MLK, se tiene que reemprender la cacería de ángulos iniciada al principio, pero ahora buscando en lugares específicos. Por ejemplo, que el ángulo A es igual al KML se logra fácilmente por lados paralelos. Y ya con la figura uno puede buscar igualdad de los ángulos KLM y APQ.
De nuevo aquí entra otro de los afectos amigos de la cognición: la persistencia (como complemento a la confianza en que la estrategia es la correcta). Así que tarde o temprano se tiene que ver que el ángulo KLM subtiende el mismo arco que el KMP (para eso está el dato de que PQ es tangente al circuncírculo de KLM). Y de ahí a ver los alternos internos KMP y MPA en las paralelas AB, MK con la transversal PM sólo hay un paso.
Se logró la semejanza buscada ¿y ahora? Bueno, ahora se emprende el camino de regreso: APQ~MLK, por lo tanto $AP/AQ=ML/MK=2ML/(2LK)=QC/PB$. Es decir, $AP\cdot PB=AQ\cdot QC$. De aquí que OP=OQ, por teorema conocido (mejor si se incluye la demostración).
Los saluda
jmd
PD: no conviene abusar de la frase "es claro que" favorita de Brandon; por ejemplo no conviene iniciar la demostración con "es claro que APQ~MLK" porque es claro que no es para nada claro que se de esa semejanza...

Pero si mal no recuerdo
Pero si mal no recuerdo demostre por que era cierta la semejanza, por el paralelismo y la tangencia del circuncirculo del triangulo MKL, por la tangencia se tiene que $\angle{MLK}=\angle{PMK}$ y por el paralelismo que $\angle{PMK}=\angle{APQ}$ y de ahi la semejanza. Lo cual si mencione en la solucion. Pero de ahora en adelante mencionare todo mas detalladamente, y tiene razon, no creo que sea facil ver esa semejanza, yo ya habia hecho un problema donde trabajaba una semejanza similae en el shariguin(creo que asi se escribe xP) y por ello supe inmediatamente que dichos triangulos eran semejantez y como probarlo, y lo demas era solo de irle buscando. Saludos
Me parece bastante
Me parece bastante interesante la explicación de las perspectivas que surgen en este particular problema. Ante esto quisiera hacer un comentario enfocado a la olimpiada de matemáticas: cuando un estudiante conoce y se interesa por los concursos tipo olimpiada, casi siempre hay un pequeño grupo de instructores (los Entrenadores) que intentan dar una base teórica sencilla y que normalmente no se ve en la escuela. Para los Entrenadores la misión imprescindible no es dar herrientas teóricas (conceptos, métodos generales de solución, propiedades y teoremas conocidos, etc), sino la de promover en el estudiante un proceso de análisis profundo a los problemas (otra cosa que no se asoma con frecuencia en el aula de la escuela). Este análisis aplicado a los problemas suele ser lo más difícil de encender en el alumno, pues es frecuente que el aprendiz ponga cierta resistencia cognitiva debido a que no es normal para el hacer eso (es común que en las escuelas exista el procedimiento educativo de "teoría - autoretroalimentación - evaluación", sin dar mucho espacio para las dudas, para el análisis, para descubrir los cómo's y los porqué's). Y dentro del análisis entran las perspectivas. Yo creo que no existe un esquema general para la resolución de los problemas (inclusive si todos son de geometría, o todos de teoría de números, etc), pero es verdad que existen perspectivas más óptimas (en esfuerzo y tiempo) que pueden ayudar al estudiante que participa en las olimpiadas (y como ejemplo claro está lo que escribió en el ensayo que la verdad me parece bastante interesante). Existen Entrenadores que prefieren por enseñar mucha teoría (tanto básica como avanzada) y realizar varios problemas aplicando únicamente esa teoría expuesta (con el análisis correspondiente); por otra parte, hay Entrenadores que optan por quedarse con teoria básica (o hasta ligeramente media sin alcanzar el nivel avanzado) y enforcarse más en el ámbito de análisis y exploración de distintos caminos de solución. En ciertas ocasiones, el conocimiento de teoría avanzada suele ser de gran ayuda, pero hay veces que un estudiante que tiene ese conocimiento se quede con ello para resolver futuros problemas, sin echarle un ojo al conocimiento básico que posiblemente considere anticuado, obsoleto (por ejemplo, el uso frecuente de relaciones e identidades trigonométricas para realizar problemas de geometría, en lugar de utilizar cacerías congruentes de ángulos y observación y análisis de figuras interesantes). Sea como sea, siempre he soñado con que un modelo de enseñanza de este tipo se pueda llevar a más escuelas (me refiero al modelo de la olimpiada, en el que se da teoría y problemas relacionados con eso, además de discusión de los estudiantes y exposición de ellos mismos).
Bueno, ya está el partido de MEX - EUA xD, veamos qué pasa (tengo fe en la selecciónm uju! :D).
Saludoz, y gracias por este artículo que está realmente interesante :D