El sábado 14 de enero iniciamos Ramón Llanos y yo un curso-taller de resolución de problemas en la UAMCEH-UAT (según la idea del post 20 problemas)
Asistieron 12 adolescentes (tres de ellos de primaria, los restantes de secundaria). Esa primera sesión sabatina estuvo a mi cargo. Así que después de la presentación del curso y de explicarles los objetivos del mismo, decidí plantearles el problema 8 del post antes mencionado (encontrar $n$ si $21n$ es un número de puros cuatros) --dado que es casi totalmente ateórico y esperando, en consecuencia, que la mayoría lo resolviera. Y así fue: después de un rato ya casi todos lo habían resuelto.
Eso me animó. Pero cuando me disponía a plantearles el problema 1 (encontrar el valor de $m^{4n}-4$ si se sabe que $m^n=3$), Ramón me dice: "sólo que no saben exponentes ¿qué tiene?". Esa información clasificada de Ramón (como profesor de secundaria) me hizo dudar (de hecho todo mi plan se derrumbaba ante esa observación). Entonces le dije: "¿tienes algún calendario infantil de problemas?". Así que Ramón se fue a su cubículo y me trajo uno del 2008, del cual elegí el siguiente problema de geometría:
Encontrar el área de la cruz de cuadrados que se muestra en la figura, dado que la diagonal de un rectángulo formado por dos cuadrados mide 6 unidades.

Los adolescentes estuvieron un rato intentando resolverlo y ninguno parecía tener idea de cómo hacerlo. Entonces les di una pista en forma de pregunta: ¿saben el Teorema de Pitágoras?
Segunda decepción: ninguno lo sabía. (Entonces, dramatizando un poco mi reacción, hice el PLOP de Condorito y, al tiempo que hacía el gesto de las manos levantadas y a punto de saltar hacia atrás, le digo a Ramón: ¡Cómo se juega esto!)
Nota: uno cree que Pitágoras es el más famoso de los matemáticos entre los escolares y los 2 millones de páginas que arroja Google lo deberían confirmar; pero esa es una falsa percepción porque Resident Evil arroja 204 millones. Sólo para comparar les pregunté: ¿quién conoce el juego Resident Evil? La mayoría levantó la mano y uno dijo: es un juego de matar zombies.
Estaba presente Luis Brandon (acompañando a su hermano, en primero de secundaria). Y, pasando al pizarrón y como respuesta a mi pregunta dramatizada a Ramón, Brandon dijo: Pitágoras se puede evitar si trazamos el cuadrado de las diagonales, al tiempo que ampliaba la figura.
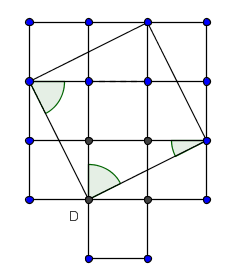
Muy bien Brandon --le dije--, y también se puede evitar si imaginamos que el cuadrado inferior lo movemos a la esquina noroeste y que trazamos otra diagonal como en esta figura (que empecé a trazar). Pero todavía falta ver si nuestros alumnos conocen el concepto de complementariedad y suplementariedad de ángulos. (Necesarios para justificar que el cuadrado al que se refería Brandon realmente es un cuadrado.)
Nota: Hay que decir que estas dos nuevas sugerencias recurren al trazo auxiliar, el cual es un artificio avanzado en el problem solving de geometría, es decir, no está al alcance de un aprendiz de menos de 15... pero, bueno fueron sugerencias y esperábamos facilitarían la resolución del problema...
En ese momento oficialicé la sugerencia de Brandon y la mía y les recordé la relación de complementariedad de ángulos, no sin antes preguntarles si sabían cuánto vale la suma de los ángulos internos de un triángulo. La mayoría sí lo sabía.
Sólo para comprobar su conocimiento de la suma de ángulos y la complementariedad les pregunté si podían decirme si, en la configuración de mi sugerencia, los ángulos son complementarios o no lo son. Varios dijeron que sí, pero al momento de justificarlo recurrían al argumento de que el ángulo que quedaba enmedio era recto y como con los otros dos forman un llano entonces... Hubo que aclararles que el ángulo que ellos veían recto podría no serlo y había que justificar que era recto.
Con toda esa ayuda los dejamos otro rato trabajando el problema. No lo resolvieron. Y como la sesión se acercaba a su fin, decidí explicarles las tres soluciones en el pizarrón en los 20 minutos que quedaban. (Lo cual --después pensé-- fue quizá excesivo. Pero, bueno, de alguna forma había que cerrar...)
La solución de Pitágoras parece que la entendieron todos. En las otras dos tuvieron sus dudas en la demostración del ángulo recto. Y en la de mi sugerencia no podían ver el trapecio que se formaba, aunque después de un rato ya lo aceptaron como trapecio. Ver siguiente figura:
Ramón me explicó que la razón estaba en que los trapecios del aula generalmente son isósceles. Lo cual interpreto como una imagen del trapecio (isósceles) fuertemente adherida a su cognición de manera que cualquier otro trapecio no es trapecio para ellos.
Enseguida formulo de manera resumida las tres soluciones:
La solución directa (o más fácil de ver) depende de la evocación del teorema de Pitágoras --después de haber reconocido el dato como la longitud de la hipotenusa. A partir de ahí el plan natural es calcular el lado de cada uno de los cuadrados aplicando Pitágoras. (El cual al final se revela innecesario pues --si llamamos $a$ al lado-- $a^2$ es ya el área de un cuadrado.) La redacción de esa solución sería más o menos así:
Solución con Pitágoras
Sea $a$ la longitud del lado de los cuadrados. Entonces la longitud de la hipotenusa es 6 y las de los catetos son $a$ y $2a$. Así que, por Pitágoras, se tiene que $a^2+(2a)^2=6^2$. Es decir, $5a^2=36$. De aquí que la respuesta sea: el área de la cruz de cuadrados es 36 unidades cuadradas.
Solución con la sugerencia de Brandon
Agregando más cuadrados se puede replicar la diagonal como se muestra en la figura. De aquí que el área del cuadrado de diagonales sea $5a^2$ --pues son cuatro triángulos rectángulos de área $a^2$ más el cuadrado del centro. Pero también es 36 --pués el área de un cuadrado es lado por lado. Así se logra la misma ecuación que se obtuvo con Pitágoras y la respuesta es 36.
Demostración de que el cuadrado de diagonales es realmente cuadrado: Para verlo basta observar que los ángulos en cada esquina del cuadrado de diagonales es la suma de dos ángulos complementarios --por ser los no rectos de un triángulo rectángulo. (Basta observar eso... ¡Pero observar eso es precisamente lo que el aprendiz no puede hacer! --pues para ello se requiere entrenamiento...)
Solución con la formación de un trapecio
Si el cuadrado inferior de la cruz de cuadrados se coloca en la esquina noroeste podemos replicar la diagonal --cuya longitud sabemos-- en el rectángulo así formado. Si ahora unimos los dos vértices que se muestran en la figura tenemos un trapecio con bases $a$ y $2a$ y altura $3a$.
Ahora calculamos el área del trapecio de dos formas y obtenemos la siguiente ecuación: $$\frac{a+2a}{2}(3a)=2\frac{a(2a)}{2}+\frac{36}{2}$$
Es decir, $5a^2=36$ y la respuesta es entonces 36.
Comentarios finales
1) La sesión fue instructiva para mí pues, como profesor de matemáticas, uno tiende a olvidar que los trucos finos del problem solving solamente se aprenden mediante el entrenamiento deliberado y poniendo un especial cuidado en dominarlos.
2) Y espero que también haya sido instructiva para ellos, pues el ambiente del aula --creado por la participación de Brandon y la interacción de él conmigo y con los alumnos-- les quedará en la memoria como uno en el que se trata de resolver un problema de varias formas. (Yo espero que también les quede en la memoria el feeling de un interés genuino por el problem solving de parte de los instructores.)
3) La enseñanza del Teorema de Pitágoras en sexto grado de primaria y tercero de secundaria pasa desapercibido para el alumno, pues podría apostar que se cubre en una sola sesión y con ejercicios de rutina. En el mejor de los casos, al alumno le queda una vaga idea de una fórmula asociada a los lados de un triángulo rectángulo (de la misma manera que recuerda Resident Evil como un juego de matar zombies)
4) En contraste con el de Pitágoras, el teorema de la suma de ángulos internos de un triángulo se puede verbalizar en una frase muy fácil de retener en la memoria: SUMAN 180. La verbalización de Pitágoras, en cambio, pasa por aprender la terminología "catetos", "hipotenusa", "suma de los cuadrados", etc
5) A pesar de que las relaciones de complementariedad y suplementariedad entre dos ángulos puede resumirse, respectivamente, en las fórmulas SUMAN 90 Y SUMAN 180 (o, equivalentemente, FORMAN UN RECTO y FORMAN UN LLANO), sus instancias de uso son no triviales --al menos para el aprendiz...
6) Al carecer de la habilidad de manipulación algebraica, la aplicación de Pitágoras no les bastaría para la solución directa. Porque todavía faltan los pasos de simplificación hasta llegar a $5a^2=36$ --en cierto momento llegué a decirles "creanme que aquí se puede cancelar"...
7) Digamos, para finalizar, que fue muy placentero para mí el haber estado a cargo de esa primera sesión sabatina del curso de resolución de problemas. Pues me parece algo extraordinario que 12 adolescentes hayan decidido dedicarle una mañana de sábado a aprender más matemáticas. Su interés genuino en aprender se reflejó en la atención sostenida prestada a los instructores y a la resolución de los ejercicios que les planteamos.
Como se sabe, el recurso más escaso en el aula es la atención de los escuelantes. Pero ese sábado, en el aula A-2 de la UAMCEH-UAT ese 14 de enero, la entregaron toda y sin reservas. Las gracias les sean dadas a esos 12 adolescentes interesados en las matemáticas. Yo espero que dos o tres de ellos hayan quedado inoculados con el meme de las matemáticas de concurso y quien quita y alguno llegue a ser campeón en un futuro no muy lejano.
Los saluda
jmd
PD: Las soluciones con trazo auxiliar dependen de una técnica estándar en matemáticas (a pesar de que siempre queda como telón de fondo): calcular de dos formas una misma cantidad (en este caso el área). Ver, por ejemplo, la definición de doble conteo.
