Geometría
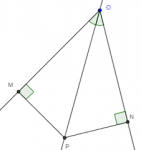
Discusión sobre incírculos y excírculos
Voy a discutir en este post algunos conceptos relacionados con las circunferencias incrita y exinscrita. Dichos conceptos forman un todo y conviene aprenderlos en paquete --es muchísimo más fácil retenerlos en la memoria y comprenderlos si se aprenden en sus interconexiones.
Se trata de los conceptos de semiperímetro --en el contexto de ciertas simetrías entre las longitudes de las tangentes de circuncírculo y excírculos--, el concepto de puntos isotómicos, y el de los puntos de Gergonne y Nagel --como ejemplo de puntos conjugados isotómicos.
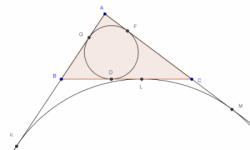
Un problema clásico de homotecia
Durante el año 2009, al final de uno de los entrenamientos de la OMM Delegación Tamaulipas, Jesús Rodríguez Viorato le planteó el siguiente problema a Luis Brandon --el líder de la selección 2009:
El incírculo de un triángulo $ABC$, es tangente en $D$ al lado $BC$ y $DM$ es un diámetro. El rayo $AM$ corta en $F$ el lado $BC$. Demostrar que $BD=CF$.
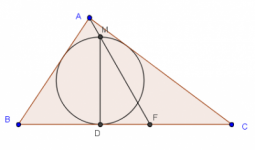
Problem solving con homotecia
Como se sabe, la perspectiva transformacional en geometría permite el movimiento de las figuras y la transferencia de propiedades desde la figura a la figura transformada. De esta manera, la utilidad principal de esta perspectiva es la simplificación del problema, a la manera de un cambio de variable en álgebra. Voy a discutir en este post el caso de la homotecia (una transformación geométrica de muy bajo perfil en las matemáticas escolares) y su uso en el problem solving elemental a través de varios teoremas básicos de la geometría.
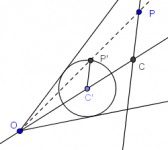
Dos problemas de construcción --con homotecia obligada
En un post anterior se plantearon dos problemas de construcción para ilustrar el poder de la homotecia en el problem solving de geometría. Aquí voy a resolverlos y a comentarlos, dado que --según creo-- merecen un post aparte. ("A: ¿Quieres decir que a la homotecia se le cocina aparte?" "JMD: Bueno, creo que lo que quiero decir es que el chiste no está en la homotecia misma, sino en saberla menear.")
Primer problema
Sea dado un ángulo y un punto en su interior. Construir una circunferencia tangente a los lados del ángulo y que pase por el punto.
Solución y discusión del primer problema
Recíproco de Tales y el criterio LAL de semejanza
El teorema de Tales para triángulos es bastante intuitivo pues recurre a la conocida configuración de las paralelas y la transversal: si paralela a la base, entonces los segmentos son proporcionales.
Sin embargo, el recíproco de Tales nos dice que si los segmentos que determina una transversal en dos lados de un triángulo son proporcionales, entonces esa transversal es paralela al tercer lado.
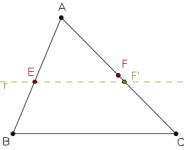
Una comunicación que calla: sobre el concepto de antiparalelas
Voy a ilustrar en este post la multiplicidad de conexiones que un cognizador debería establecer con una teoría previa en el momento de resolver (o estudiar la solución a) un problema de matemáticas escolares. Sostengo que la forma condensada de presentar las soluciones es una forma reticente de comunicar --así sea de manera involuntaria o por razones de estilo de redacción.
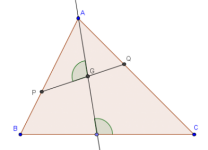
El cuadrado de Polya --con Geogebra
En este post comento sobre un posible proceso de solución al problema clásico de inscribir un cuadrado en un triángulo, usando el software de geometría dinamico Geogebra.
El cuadrado de Polya
En el problem solving de las matemáticas escolares hay algunos problemas que son ya legendarios. Uno de ellos es el problema del cuadrado de Polya. Se trata de inscribir un cuadrado en un triángulo. A continuación su enunciado:
Inscribir un cuadrado en un triángulo $ABC$. Dos de los vértices del cuadrado deben estar en la base $BC$, y los otros dos en los otros dos lados, uno en cada uno.
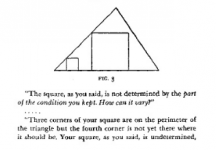
Dualidad en geometría