Geometría
Cuadrilátero cíclico --criterios e instancias de uso
Puesto que el material disponible en la Web sobre los cuadriláteros cíclicos no incluye las demostraciones de los criterios de su reconocimiento (con excepciones difíciles de encontrar) voy a presentar en este post los tres criterios para el reconocimiento de un cuadrilátero cíclico, así como sus demostraciones. Añado tres instancias de uso.
Definición y criterios de reconocimiento
Primero la definición:
Si los cuatro vértices de un cuadrilátero convexo están sobre la misma circunferencia, entonces se dice que el cuadrilátero es cíclico.
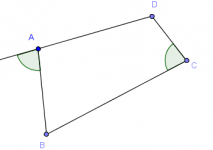
El difícil de la ONMAPS --Tamaulipas 2014
La caja de Arquímedes: un rompecabezas milenario

Soluciones múltiples para un problema geométrico
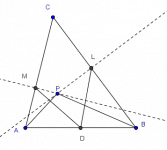
Una vez superada la cuesta de enero encontré este problema de geometría en la Web el cual comparto con los lectores de MaTeTaM. Doy la solución vectorial y varias sugerencias para soluciones sintéticas. (La idea es recomendar a los cognizadores preparándose para concursos de matemáticas escolares a no abandonar un problema después de obtener una solución. Buscar otras soluciones los hará más sabios en el arte del problem solving.)
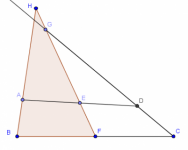
Problem solving con vectores --2a parte
En este post voy a continuar el post anterior sobre vectores añadiendo dos operaciones adicionales a las ya abordadas (suma y resta y multiplicación por un escalar).
Se trata del producto interior (o escalar o punto) entre dos vectores y el producto área (o exterior o cruz), los cuales aportan, respectivamente, sendos criterios para la perpendicularidad y la colinealidad de vectores. Se discuten algunas instancias de uso para demostrar el potencial de los vectores en el problem solving de geometría. Voy a iniciar con un
Problem solving con vectores
En este post voy a argumentar a favor del uso de los vectores en el problem solving en geometría. Con las definiciones iniciales de vector, vectores de posición, vectores libres, igualdad de vectores, y la suma y resta de vectores presento la demostración de varios teoremas de la geometría como instancias de uso de esta poderosa herramienta. Destacan las instancias de uso finales sobre la demostración puramente vectorial de la fórmula de Sylvester y de la Recta de Euler.

Un problema de geometría --de Wong Yan Loi
En su libro Introduction to geometry, Wong Yan Loi presenta el problema motivo de este post (y lo resuelve con geometría analítica). La redacción del enunciado está aquí ligeramente modificada y a la solución le he añadido explicaciones que Wong Yan Loi se ahorra. (Me gustaría ver una solución sintética de este problema. Si alguien la encuentra sería una buena obra que la compartiera con los lectores de MaTeTaM.)
El 5 del VI concurso nacional OMM 1992
Cuando llueve, como en estos días que se formó en el Golfo de México la tormenta Ingrid, me pongo inspirado y con ganas de postear. Buscando qué hacer mientras llovía me encontré con este problema del concurso nacional de 1992 (VI OMM).
Teorema fundamental de la proporcionalidad (Tales)
Si una recta paralela al lado $BC$ del triángulo $ABC$ corta en $B'$ a $AB$ y en $C'$ a $AC$), entonces $$\frac{AB}{AB'}=\frac{AC}{AC'}=\frac{BC}{B'C'}$$
Este es el Teorema de Tales para triángulos del cual hemos hablado ya en MaTeTaM. En esta oportunidad comentaré el teorema particularizado para triángulos rectángulos y lo demostraré con el método de áreas.
Segunda lección: complementos
En este post, dirigido a los alumnos del curso, propongo resolver 11 problemas de geometría elemental. Las dudas expresarlas en comentarios.
1. Encontrar la longitud de la altura de un triángulo equilátero de lado $8\sqrt{21}$. Sugerencia:Pitágoras.
2. Utilizando el teorema de Pitágoras, demostrar que la altura de un triángulo equilátero es también mediana (y, por tanto, mediatriz y bisectriz).