Cuando llueve, como en estos días que se formó en el Golfo de México la tormenta Ingrid, me pongo inspirado y con ganas de postear. Buscando qué hacer mientras llovía me encontré con este problema del concurso nacional de 1992 (VI OMM).
Y aunque el inciso a) se resuelve en tres patadas, al b) no le hallaba la clave de su solución. Así que lo intenté con geometría analítica y, para mi sorpresa, el problema rindió sus armas sin ofrecer resistencia. Enseguida el problema y su solución. (Juzguen los lectores el poder de la herramienta analítica.)
Sea $ABCD$ un rectángulo. Sean $I$ el punto medio de $CD$ y $M$ la intersección de $BI$ con la diagonal $AC$.1. Pruebe que $DM$ pasa por el punto medio de $BC$.
2. Sea $E$ el punto exterior al rectángulo tal que $ABE$ es un triángulo isósceles rectángulo en $E$. Además, supongamos que $BC = BE = a$. Pruebe que $ME$ es bisectriz del ángulo $AMB$.
3. Calcule el área del cuadrilátero $AEBM$ en función de $A$.
Solución (con geometría analítica)
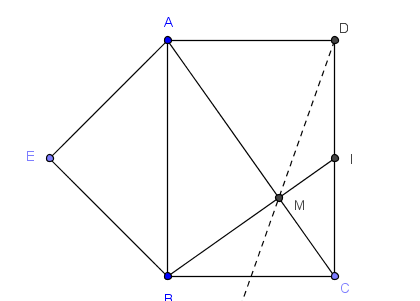
Supongamos que $BC$ mide $a$ unidades y $BA$ mide $b$. Ubicando el origen de coordenadas en $B$, es natural tomar el eje $X$ como la recta $BC$ y el eje $Y$ como la recta $BA$. Entonces, las coordenadas de los vértices relevantes para el problema son:
$$\begin{eqnarray}
A&=&(0,b)\\
B&=&(0,0)\\
C&=&(a,0)\\
I&=&(a,b/2)\\
D&=&(a,b)
\end{eqnarray}$$
a)Para demostrar que $DM$ pasa por el punto medio de $BC$ calcularemos la ecuación de la recta $DM$ --para después calcular la abscisa de la intersección con el eje $X$. Pero para calcular esa ecuación, primero debemos calcular las coordenadas de $M$ (como la intersección de $AC$ y $BI$).
Cálculo de las coordenadas de $M$
Claramente la recta $AC$ tiene pendiente $-b/a$ y $b$ es su ordenada al origen. Por tanto:
Ecuación de la recta $AC$: $y=-bx/a+b$
Ecuación de la recta $BI$: $y=bx/(2a)$
Igualando ordenadas se obtiene
$$b=(\frac{b}{a}+\frac{b}{2a})x$$
Despejando la $x$ se obtiene
$$x=\frac{2ab}{3b}=\frac{2a}{3}$$ y $$y=\frac{b}{3}$$
Por tanto
$$M=(\frac{2a}{3},\frac{b}{3})$$
De aquí que la ecuación de $DM$ sea
$$\frac{y-b}{x-a}=\frac{b/3-b}{2a/3-a}$$
Sin simplificar, hagamos en esta ecuación $y=0$. Al despejar $x$ se obtiene $x=a/2$. Es decir, $DM$ pasa por el punto medio de $BC$.
(Alternativamente, si uno focaliza el triángulo $BCD$, es fácil darse cuenta que $BI$ es mediana --por dato. Y como las diagonales de un paralelogramo se bisecan, $CM$ también es mediana. Por tanto, $M$ es baricentro y, en consecuencia, $DM$ es también mediana. Es decir, pasa por el punto medio de $BC$.)
b) Con el dato adicional para este inciso, $b^2=2a^2$ (por Pitágoras). Por tanto, $b=\sqrt{2}a$. Con esta nueva información, no es difícil darse cuenta que las rectas $AM$ y $BM$ son perpendiculares. Pues la pendiente de $AM$ es $-b/a$, es decir, $-\sqrt{2}$; y la de $BM$ es $1/\sqrt{2}$.
Pero entonces el cuadrilátero $AEBM$ es cíclico. Ahora bien, para ver que $EM$ es bisectriz del ángulo $AMB$ basta con darse cuenta de que $AE$ y $EB$ son cuerdas de la misma longitud del circuncírculo de $AEBM$ (y recordar que a cuerdas iguales arcos iguales).
c) Para calcular el área del cuadrilátero $AEBM$ usaremos el procedimiento del determinante. (Claramente las coordenadas de $E$ son $(-\sqrt{2}a/2,\sqrt{2}a/2)$.) Entonces
$$(ABM)=\frac{1}{2}\left|\begin{array}{ccc}
0 & \sqrt{2}a &1 \\
2a/3 & \sqrt{2}a/3 & 1\\
0 & 0 & 1
\end{array} \right| =\sqrt{2}a^2/3$$
$$(AEB)=\frac{1}{2}\left|\begin{array}{ccc}
0 & \sqrt{2}a &1 \\
-\sqrt{2}a/2 & \sqrt{2}a/2 & 1\\
0 & 0 & 1
\end{array} \right| =a^2/2$$
Por tanto $$(AEBM)=\frac{(3+2\sqrt{2})a^2}{6}$$
Comentarios finales
1. El primer inciso es elemental (aplicando concurrencia de medianas) y ello podría hacer pensar que los siguientes también lo son. Pero no. Uno se puede quedar mucho tiempo buscando la clave de la solución del segundo inciso sin llegar a verla. E incluso si uno conjetura que $AEBN$ es cuadrilátero cíclico, y que por ello el ángulo $AMB$ debería ser recto.Aún así decía, no es fácil ver cómo demostrar perpendicularidad.
2. Y es que la clave para demostrarlo es el tercer criterio de semejanza, uno de los criterios que oculta con frecuencia su presencia en una configuración geometrica (ver el problema geométrico propuesto por Orlando Ochoa ). Nótese:
$$\frac{AC}{DC}=\frac{\sqrt{3}a}{\sqrt{2}a}=\sqrt{\frac{3}{2}}$$
$$\frac{CI}{MC}=\frac{\frac{\sqrt{2}a}{2}}{\frac{\sqrt{3}a}{3}}=\sqrt{\frac{3}{2}}$$
3. En un análisis posterior a la solución aquí presentada me di cuenta que, como el tercer inciso pide el área entonces ello debería conducir a pensar que no hay otra que calcular longitudes. Y si uno concluyera esto, posiblemente concluiría también la posible aplicación del tercer criterio (un ángulo compartido y lados proposcionales).
4. Notemos, finalmente, que la geometría analítica no ahorra el razonamiento sintético. Se tiene que elaborar el plan de solución y sacar conclusiones de los resultados, de acuerdo a teoremas básicos. Es decir los resultados de los cálculos hay que interpretarlos. Y esto queda fuera de la herramienta analítica.
Los saluda
jmd
