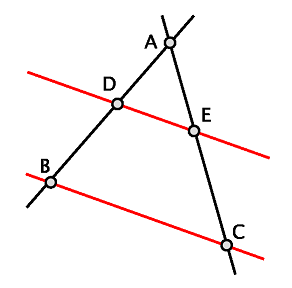
Notemos que los triángulos $ADE$ y $ADC$ tienen la misma altura (respecto al lado $AC$). Análogamente, los triángulos $AED$ y $AEB$ tienen la misma altura (respecto al lado $AB$). También notemos que los triángulos que se forman entre las paralelas $DE$ y $BC$ ($BCD, BCE, DEB, DEC$) tienen la misma altura. Se tiene entonces la siguiente cadena de igualdades:
$$AB/AD=(AEB)/(AED)=[(ABC)-(BCE)]/(AED)$$
$$=[(ABC)-((BCD)]/(ADE)=(ADC)/(ADE)=AC/AE$$
No es parte del teorema de Tales, pero se puede demostrar la equivalencia de Tales y la semejanza de triángulos demostrando que las paralelas están también en la misma razón. Véase:
Para demostrar la proporcionalidad de las paralelas llamemos $k$ al cociente de las razones iguales $AB/AD=AC/AE=k$. Es decir, $AB=kAD$, $AC=kAE$. Y también, aplicando lo que acabamos de demostrar, $H=kh$ (donde $H$ y $h$ son las alturas respecto a las paralelas de los triángulos $BCA$ y $DEA$, respectivamente). De aquí que
$$AB/AD=(ABE)/(ADE)=[(ABC)-(BCE)]/((ADE)$$
$$=[BC(kh)/2-BC(kh-h)/2]/DE(h/2)$$
$$=[kBC-(k-1)BC]/DE=BC/DE$$.
Finalmente, veamos que pasa si la paralela corta a los lados en su prolongación:

Para demostrar que también así la paralela divide a los lados en la misma razón, tomemos el simétrico $D'$ de $D$ respecto al vértice $A$ y el simétrico $E'$ respecto al vértice $A$. (Se pide al lector aportar la figura.) Aplicando Tales con la paralela $D'E'$ se obtiene $AB/AD'=AC/AE'$. Es decir, por la simetría central, $AB/AD=AC/AE$. Si ahora sumamos 1 en cada lado de esta ecuación se obtiene $BD/DA=CE/EA$. (Recordemos que la división de un segmento en una razón dada no ncesariamente tiene que ser con un punto entre los extremos del segmento. Ver teoremas de Menelao y Ceva.)
Tales en tres pasos:

Paso 1:
En el lado $AC$ tienen su base los triángulos $ACB$ y $ECB$ y tienen la misma altura. Por tanto $(ACB)/(ECB)=AC/EC$.
Paso 2:
En el lado $AB$ tienen su base los triángulos $ABC$ y $DBC$ y tienen la misma altura. Por tanto $(ABC)/(DBC)=AB/DB$.
Paso 3:
Pero los triángulos $ECB$ y $DBC$ tienen la misma área. Por tanto, $AC/EC=AB/DB$. (Y restando 1 en ambos lados, se obtiene $AD/DB=AE/EC$.)
El teorema de Tales es casi
El teorema de Tales es casi un axioma (el razonamiento proporcional parece estar en el genoma) y se puede usar por el aprendiz sin ningún remordimiento. Es, sin embargo, un buen ejercicio demostrarlo mediante el método de áreas usado aquí. Un buen ejercicio por varias razones, pero sobre todo para agudizar la visualización de triángulos relevantes para la resolución del problema en la configuración geométrica correspondiente. La visualización requiere entrenar la mirada para ver lo que se necesita ver.
Los saluda
jmd
PD: Una prueba de la fama del teorema de Tales (dentro de ciertos círculos sociales) está en este video de Les Luthiers
Hola Maestro Muñoz. Tengo una
Hola Maestro Muñoz.
Tengo una pregunta respecto a este video. El video dice algo así:
"Si tres o más paralelas son cortadas por dos transversales... "
Pero el enunciado que usted pone dice una cosa distinta. Mis duda es:
¿A qué se debe esta diferencia de enunciados?¿Son equivalentes?¿Cuál enunciado es más parecido al original dicho por Tales?
Saludos
Jesús: Has asumido a la
Jesús:
Has asumido a la perfección el papel del aprendiz que el profesor de matemáticas busca permanentemente --como Diógenes con su lámpara-- en las aulas escolares. Es decir, al aprendiz que interroga al profesor y/o al texto de tal manera que al profe lo pone a estudiar y al texto le da vida.
El teorema de Tales que publico en MaTeTaM es la versión de Euclides (libro 6, proposición 2). Por favor consulten el excelente trabajo de edición de la versión electrónica:
http://www.euclides.org/menu/elements_esp/06/proposicioneslibro6.htm
(Este sitio dedicado a Los Elementos de Euclides, me ha dejado maravillado. Lo recomiendo sin reservas a todos los adolescentes ineteresados en las matemáticas de concurso.)
El teorema de Tales que inicia --como la pieza de Les Luthiers-- "si tres o más paralelas...", puede considerarse un corolario de la versión de Euclides. (Curiosamente, ninguno de los 5 teoremas que la Británica atribuye a Tales es alguno de estos dos.) Me ahorro la figura:
Sean A, B, C los puntos de intersección de la primera transversal con tres de las paralelas dadas, y A', B', C' los correspondientes de la segunda transversal. Si las transversales son paralelas, se forman dos paralelogramos y el resultado es obvio. Si no son paralelas, entonces trazamos una paralela a la segunda transversal por A con, digamos, intersecciones B'', C'' en la segunda transversal. Ahora aplico la versión de Euclides de Tales y obtengo AC/AB=AC''/AB''=A'C'/A'B'. Es decir, AC/AB=A'C'/A'B'. Si ahora resto 1 en cada lado de esta proporción, obtengo la proporción BC/AB=B'C'/AB'. Es decir, la que Les Luthiers enuncian al principio de su canción:
Si tres o más paralelas, si tres o más parale-le-le-las
Si tres o más paralelas, si tres o más parale-le-le-las
Son cortadas por dos transversales
Son cortadas por dos transversales
Si tres o más parale-le-le-las
Son cortadas, son cortadas
Dos segmentos de una de estas, dos segmentos cualesquiera
Dos segmentos de una de estas son proporcionales
a los dos segmentos correspondientes de la otra.
Los saluda
jmd