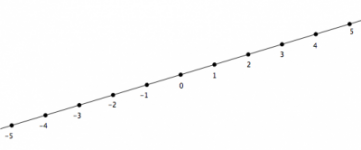
Geometría
Juego de evocaciones (en un problema de ENLACE bachillerato)
Si bien en la escuela mexicana no es necesaria la eficacia en el problem solving, ésta sí es relativamente importante en los exámenes estandarizados que miden actualmente el desempeño escolar de los adolescentes en matemáticas. Por ejemplo el examen ENLACE --Evaluación Nacional del Logro Académico en Centros Escolares. (ENLACE es importante pues se trata de una mirada externa al quehacer de la escuela y, con un poquito de vergüenza, es muy difícil ignorar su importancia.)
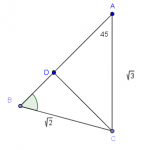
Ecuación de la recta
Tres conceptos básicos de la geometría analítica
PISA 2009, OCDE-recomendaciones 2010, y efecto Casandra
En este post sugiero la razón por la que una de las recomendaciones de la OCDE para evitar el triste futuro (y presente) educativo de México es imposible de realizar, e incluyo uno de los problemas de matemáticas de PISA 2009, la evaluación internacional de la OCDE que mide el estado de la educación de los países miembros.
Sobre el principio de no contradicción
El año pasado, al iniciar los entrenamientos de la preselección Tamaulipas para la Olimpiada Mexicana de Matemáticas, les presenté a los preseleccionados el "teorema" clásico de que todos los triángulos son isósceles (Ver mi post Lapsus de razonamiento para una "demostración" ).
Después de presentar la figura a mano alzada en el pizarrón (de hecho, la figura es la fuente de toda la confusión) Luis Brandon pasó al frente y realizó la "demostración" (pues ya la conocía y sabía que estaba trucada).
Sentido de la estructura geométrica
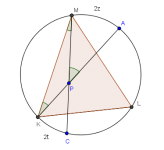
Relación entre la razón de semejanza y la razón de áreas
Inspirado por la solución de Luis Germán al Problema 7 (Ciudades, OMM_Tam_2010) decidí escribir este post. En su solución, Luis Germán usa un resultado conocido pero que pocos se dan cuenta de su importancia. Este resultado, aunque elemental, permite atajar muchísimo la solución a algunos problemas. Con este resultado, Germán pudo calcular el área del triángulo en cuestión sin tener que calcular todos sus lados.
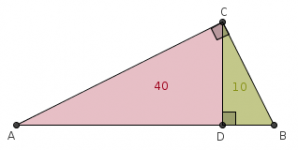
El diagrama: ¿facilita realmente el razonamiento?
La respuesta a la pregunta del título es: depende del razonador. Esta respuesta la derivé de una experiencia de enseñanza que a continuación narro y comento.
En estos días, dentro del tema de geometría, traté de enseñarles a dos jóvenes universitarios el teorema de Pitágoras. Es decir, la demostración de ese famoso teorema. Fue de hecho un experimento didáctico, solamente para comprobar que a un estudiante profesional (es decir, que el ser estudiante ha sido su modus vivendi por al menos 13 años) le resulta casi imposible concentrarse en una tarea de este tipo.

Reto para novicios: el problema 4 de la IMO 2009 (invertido y con 4 incisos)
Aprovechando el entusiasmo de Brandon voy a poner aquí una variante del problema 4 de la IMO 2009, desglosándolo e invirtiéndolo con la idea de reducir su complejidad. Pero antes de plantear el reto a los miembros de la preselección Tamaulipas 2009, permítaseme comentar dos o tres cosas sobre ese problema, sobre su dificultad.
Segmentos Dirigidos
Este concepto se oye mucho en las Olimpiadas de Matemáticas, pero --como muchos otros de olimpiada-- no es un tema que se enseñe en bachillerato. Esto puede llegar a asustar a muchos estudiantes, pero en realidad es un tema al que nada hay que temerle. Es muy fácil de entender y sobre todo es muy útil.
La idea principal de los segmento dirigidos es agregar una propiedad extra a la noción de segmento. Esta propiedad se resume así: