
Si bien en la escuela mexicana no es necesaria la eficacia en el problem solving, ésta sí es relativamente importante en los exámenes estandarizados que miden actualmente el desempeño escolar de los adolescentes en matemáticas. Por ejemplo el examen ENLACE --Evaluación Nacional del Logro Académico en Centros Escolares. (ENLACE es importante pues se trata de una mirada externa al quehacer de la escuela y, con un poquito de vergüenza, es muy difícil ignorar su importancia.)
En este post discuto el significado de evocación como un traer a presencia y propongo que ese traer a presencia debería ser construido de manera deliberada con miras a mejorar la eficacia en el problem solving en matemáticas escolares. Se propone el ejemplo de los triángulos rectángulos notables para un diseño de la evocación de sus propiedades a partir de los datos en un problema y se aplica en 4 tareas de aplicación directa y un problema de ENLACE Bachillerato 2010.
La evocación de un concepto como un traer a presencia a partir de un signo
Como significado primario, evocación es la fórmula ritual que el hechicero pronuncia para hacer presente el alma de los muertos. Pero para este significado se prefiere la palabra conjuro (fórmula mágica que se recita para conseguir algo o alejar algún peligro) o invocación (petición a una deidad). Sin embargo, por extensión, evocar significa (según la real academia española) traer algo a la memoria o a la imaginación.
Y si combinamos ambos significados,
evocación significaría (en el problem solving) una especie de traer a presencia (a la memoria) un concepto o procedimiento que posiblemente sea útil para resolver un problema.
Ahora bien, ese traer a presencia un concepto o procedimiento, o el hecho de que el concepto se haga presente en nuestra memoria, no siempre es un acto voluntario, sino que con frecuencia la presencia del concepto o procedimiento es provocada o activada mediante un signo o señal en el enunciado del problema. (Un fenómeno que el experto no hace consciente porque ya está integrado en la estructura de su base de conocimientos, pero que está en proceso de formación en el novicio que aspira a ser experto --y ese proceso necesita ser autogestionado de manera activa y deliberada.)
Y si aceptamos (así sea de manera provisional) que así es como funciona la memoria y la evocación, entonces es posible facilitar a la memoria espontanea su hacer, tratando de crear en nuestra mente asociaciones entre el concepto y el signo que lo evoca (crear una evocación diseñada). Un ejemplo es el de los triángulos 30-60-90 y el isósceles rectángulo (dos de los denominados triángulos rectángulos notables más usados en el problem solving de geometría).
El mecanismo de evocación que sugiero construir (al adolescente interesado en las matemáticas) para usar de manera eficaz estos dos triángulos rectángulos notables es el siguiente:
- signo evocador: $\sqrt{3}$; concepto evocado: triángulo 30-60-90.
- signo evocador: $\sqrt{2}$; concepto evocado: triángulo isósceles rectángulo.
Una forma fácil de retener en la memoria las características de estos dos triángulos es pensarlos como la mitad de un equilátero de lado 2 y la mitad de un cuadrado de lado 1. (Otro de los triángulos rectángulos notables es el 3k-4k-5k, en el cual los ángulos no rectos miden 53 y 37 grados.)
Cuatro tareas (instacias de uso) de la evocación de triángulos rectángulos notables
- a) La hipotenusa de un triángulo rectángulo mide 10 unidades y uno de sus ángulos mide 37 grados. ¿Cuánto miden los catetos?
- b) Un cateto mide 9 unidades y un ángulo mide 45 grados. ¿Cuánto miden la hipotenusa y el otro cateto?
- c) La hipotenusa mide 18 unidades y un ángulo 60 grados. ¿Cuánto miden los catetos?
- d) Un cateto mide 26 y un ángulo 30. ¿Cuánto miden el otro cateto y la hipotenusa?
En los textos escolares de geometría se suele pedir al lector memorizar los triángulos rectángulos notables. Pero si no se le presentan instancias de uso, el lector no sabría qué memorizar. Las instancias anteriores --creo-- aclaran la idea de qué es lo que hay que memorizar de los triángulos rectángulos notables.
Instancia de uso (adaptada de ENLACE Bachillerato 2010)
El ángulo $A$ del triángulo $ABC$ mide 45 grados, el lado opuesto $BC$ mide $\sqrt{2}$, y el adyacente $AC$ mide $\sqrt{3}$. Encontrar la medida del ángulo $CBA$.
Nota: En ENLACE Bachillerato 2010 se da la figura y cuatro opciones para elegir una como respuesta, lo cual está lejos de hacer más fácil el problema. La figura es la siguiente (ya incluido el trazo auxiliar $AD$ sugerido por el juego de evocaciones):
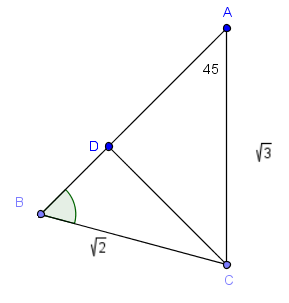
Análisis del problema de ENLACE 2010
Los datos evocan un triángulo rectángulo isósceles y un 30-60-90. El rectángulo isósceles es activado por dos signos: $\sqrt{2}$ y por el ángulo de 45 grados. El 30-60-90 es evocado a través del dato $\sqrt{3}$.
Sin embargo, el dato $\sqrt{3}$ no lleva a un 30-60-90, pues un ángulo es de 45. Entonces hay que hacer una corrección a la evocación inicial: el verdadero signo de la evocación es el ángulo de 45. Y éste evoca la mitad de un cuadrado (que hay que construir). Por esa razón...
Solución al problema de ENLACE 2010
Sea $D$ el pie de la perpendicular bajada desde $C$ al lado $AB$. Entonces, como $\sqrt{3}=\sqrt{6/2}=\sqrt{2}\sqrt{3/2}$, el lado $CD$ debe medir $\sqrt{3/2}$ (esto también es verificable con Pitágoras).
Y aquí lo más directo es aplicar trigonometría:
$$senx=\sqrt{3/2}/\sqrt{2}=\sqrt{3}/2$$
Y se sigue que el ángulo buscado es de 60 grados --evocando la mitad de un equilátero, es decir, el 30-60-90.
Solución a las instancias de uso (de evocación de triángulos rectángulos notables)
- a) ¿Uno de los ángulos es de 37? ¡Ah! Entonces es un triángulo 3k-4k-5k, con k=2 (pues la hipotenusa mide 10=5(2)). De aquí que los catetos miden 6 y 8.
- b) ¿Ángulo de 45? ¡Ah! Entonces es un isósceles rectángulo. Por lo tanto sus catetos miden ambos 9 unidades, y la hipotenusa $9\sqrt{2}$
- c) ¿Ángulo de 60? ¡Ah! Entonces es la mitad de un equilátero (un 30-60-90). Por tanto uno de los catetos mide 9 (la mitad de la hipotenusa) y el otro $9\sqrt{3}$ (verificable también por Pitágoras).
- d) Puesto que 26=2(13) no involucra $\sqrt{3}$, entonces se trata del cateto que mide la mitad de la hipotenusa. Por tanto, ésta mide 52 unidades. El otro cateto mide entonces $26\sqrt{3}$
Los saluda
jmd
PD: Por trigonometría, el trazo auxiliar $CD$ queda sugerido en el mero intento de calcular el seno del ángulo ($CD/\sqrt{2}$). Una vez haciendo el trazo auxiliar $CD$, éste se calcula de nuevo por el seno (de 45 grados). Pero aquí hay que evocar el isósceles rectángulo, para concluir que $CD=\sqrt{3}\frac{1}{\sqrt{2}}$. La cadena de cálculos sería como sigue:
$sen{x}=\frac{CD}{\sqrt{2}}=\frac{\sqrt{3}sen{45}}{\sqrt{2}}=\frac{ \sqrt{3}\frac{1}{\sqrt{2}}}{\sqrt{2}}=\frac{\sqrt{3}}{2}$
Por tanto, $x=60$ grados --evocando el 30-60-90.
Nótese que un abordaje directo por trigonometría no ahorra la evocación de los triángulos rectángulos notables --a menos que se permita la calculadora. Sin calculadora ni conocimientos previos sobre los triángulos rectánglos notables, el problema es imposible. Ver mi post
Con trigonometría (a veces) la creatividad es innecesaria.

