Puesto que el material disponible en la Web sobre los cuadriláteros cíclicos no incluye las demostraciones de los criterios de su reconocimiento (con excepciones difíciles de encontrar) voy a presentar en este post los tres criterios para el reconocimiento de un cuadrilátero cíclico, así como sus demostraciones. Añado tres instancias de uso.
Definición y criterios de reconocimiento
Primero la definición:
Si los cuatro vértices de un cuadrilátero convexo están sobre la misma circunferencia, entonces se dice que el cuadrilátero es cíclico.
Ahora bien, si los vértices no están visualmente sobre una circunferencia, necesitamos criterios para decidir si es el caso de que estén en una circunferencia. Visualmente, los criterios son los siguientes:

¿Ángulos opuestos suplementarios? Entonces es cíclico.
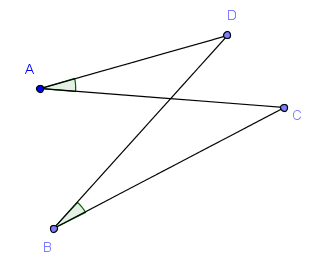
¿Lados opuestos y diagonales forman ángulos iguales? ¡Cíclico!
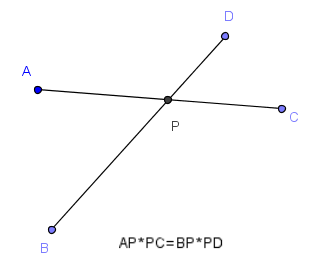
¿Cómo se verbaliza esto?
Los criterios y sus demostraciones
Criterio usual y su demostración
Un cuadrilátero es cíclico si y sólo si sus ángulos opuestos son suplementarios.
Demostración
Si un cuadrilátero es cíclico entonces los arcos interceptados de ángulos opuestos suman toda la circunferencia, es decir, 360 grados. Por tanto, sus correspondientes ángulos centrales suman la mitad, es decir, dos rectos.
Para la conversa, supongamos que los ángulos opuestos de un cuadrilátero son suplementarios (digamos el B y el D). Tracemos el circuncírculo de ABC y sea D' el punto de intersección de AD con la circunferencia trazada.
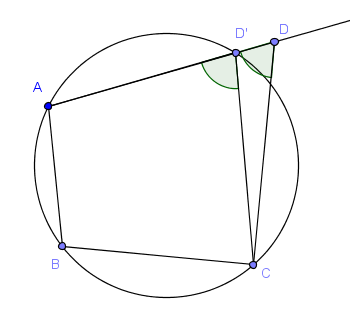
Entonces, por hipótesis, $\angle{ABC}+\angle{ADC}=180$. Pero, por lo que acabamos de demostrar, $\angle{ABC}+\angle{AD'C}=180$.
De aquí que $\angle{AD'C}=\angle{ADC}$. Y hemos llegado a la absurda situación en que el ángulo externo de un triángulo es igual a uno de los no adyacentes --absurda, a menos que D y D' coincidan...
Criterio no tan usual
Un cuadrilátero ABCD es cíclico si y sólo si $\angle{CAD}=\angle{CBD}$ (dos lados opuestos forman ángulos iguales con las diagonales).
Demostración
Si el cuadrilátero ABCD es cíclico entonces los ángulos $\angle{CAD}$ y $\angle{CBD}$ tienen el mismo arco interceptado. Por tanto son iguales.
Para la conversa, supongamos que $\angle{CAD}=\angle{CBD}$ y llamemos P a la intersección de las diagonales. Debería ser claro que los triángulos APB y DPC son semejantes (pues sus ángulos correspondientes son iguales).
Pero también son semejantes los triángulos APD y BPC (por el tercer criterio). Y se llega fácilmente a que los ángulos opuestos del cuadrilátero ABCD son suplementarios.
Criterio de la potencia de la intersección de diagonales
Un cuadrilátero ABCD es cíclico si y sólo si $AP\cdot{PC}=BP\cdot{PD}$ --donde P es la intersección de las diagonales.
Demostración
Si el cuadrilátero es cíclico entonces, por definición, sus vértices están sobre una circunferencia. Y entonces debe cumplirse que la potencia de P se expresa como se dice en la conclusión.
Para la conversa, supongamos que $AP\cdot{PC}=BP\cdot{PD}$, con P la intersección de AC y BD. Pero esa ecuación es equivalente a la proporción $AP/BP=DP/PC$. De aquí que, por el tercer criterio, los triángulos APB y DPC son semejantes --pues $\angle{APB}=\angle{CPD}$.
Pero $AP\cdot{PC}=BP\cdot{PD}$ es también equivalente a AP/DP=BP/PC, y se llega a que los triángulos APD y BPC son también semejantes. El argumento restante es similar al de la demostración del segundo criterio.
Instancias de uso
Criterio usual:
En la figura, M es el punto medio de la cuerda PQ, O es el centro del círculo y E y F son los puntos medios de AD y CB, respectivamente. Demostrar que los cuadriláteros JMOE y KMOF son cíclicos.

Solución
Es inmediata, al observar que, en ambos, dos de sus ángulos opuestos son rectos
Criterio no tan usual:
En la figura, M es el punto medio de la cuerda PQ y RS es paralelo a AD. Demostrar que el cuadrilátero RCSB es cíclico.
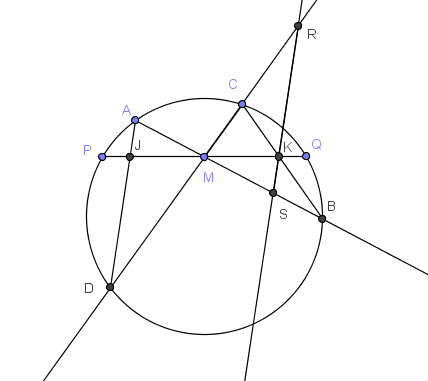
Solución
Los ángulos CBA y CDA son iguales (mismo arco). Pero, por alternos internos, son también iguales al ángulo CRS.
Criterio usual (escondido)
En la figura, M es punto medio de la cuerda PQ, O es el centro del círculo y D' es el reflejo de D en la recta OM. Demostrar que el cuadrilátero D'BKN es cíclico.
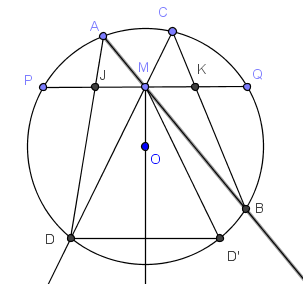
Solución
Viendo el cíclico DD'BC, es claro que los ángulos D'DM y D'BC son suplementarios. Pero el D'DM es igual al D'MK (alternos internos). Por tanto, el cuadrilátero D'BKN es cíclico.
Se atachan en png tres demostraciones del teorema de la mariposa que es de donde saqué las instancias de uso de los cuadriláteros cíclicos.
Los saluda
jmd
PD: Para la instancia de uso que denominé criterio no tan usual (escondido), es interesante notar que si reflejamos B en la mediatriz de PQ, la forma en que identificamos el cíclico JMDB' puede ser muy difícil de ver.
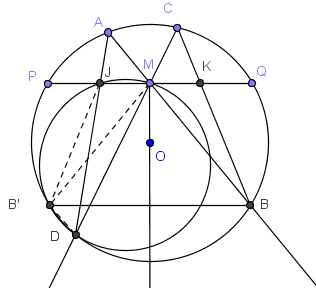
En la figura siguiente se sombrean los ángulos iguales. Su identificación sucede en dos momentos: derecha, izquierda y arriba a la derecha por isósceles y alternos internos; derecha y abajo a la izquierda por mismo arco interceptado.

| Adjunto | Descripción | Tamaño | |
|---|---|---|---|
| 1_mariposa.png | Primera demostración del teorema de la mariposa | 149.63 KB | |
| 2_mariposa.png | Segunda demostración del teorema de la mariposa | 124.63 KB | |
| 3_mariposa.png | Tercera demostración del teorema de la mariposa | 145.55 KB | |
