Debería ser claro que el cuadrilátero BMPN es cíclico (ángulos opuestos de 60 y 120). De aquí que P está en el circuncírculo de BMN. Llamemos O al centro del triángulo y O(P) al circuncentro de BMN. (Notemos que O(P) depende de la ubicación de P al determinar éste los puntos M y N.)
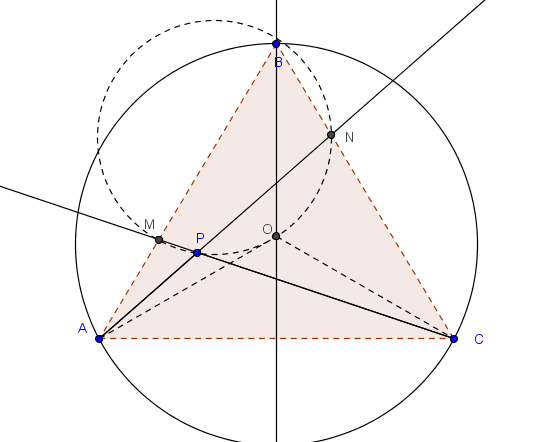
Es relativamente fácil darse cuenta que el ángulo AOC mide 120 grados (pues O es la intersección de las bisectrices y forma el isósceles AOC de 30-120-30). Por tanto, la trayectoria de P pasa por el centro O de ABC.
Una consecuencia de este hecho (que el ángulo AOC es de 120) es que el cuadrilátero APOC es cíclico (suponiendo P del mismo lado que A respecto a la bisectriz de B) de acuerdo al criterio de los ángulos inscritos.
Siendo APOC cíclico, los ángulos CPO y CAO subtienden el mismo arco OC. Es decir, miden ambos 30 grados. Pero entonces el cuadrilátero BOPM es también cíclico (opuestos de 30 y 150). En resumen, tanto P como O pertenecen al circuncírculo de BMN.
Tenemos entonces que dos puntos fijos (el B y el O) pertenecen al circuncírculo de BMN. Así que se puede afirmar que el circuncentro O(P) de BMN se mueve sobre la mediatriz de la cuerda OB.
Pero como P se mueve sobre el arco capaz de 120 respecto al segmento AC, entonces P recorre ese arco desde A hasta C (en el interior del triángulo ABC). Esto significa que el lugar geométrico del circuncentro MBN al variar P es el segmento sobre la mediatriz de OB que forma un rectángulo con AC.

Como se puede observar $BMPN$
Como se puede observar $BMPN$ es ciclico de alli $BMC \equiv CNA$ entonces $CN=BM$ como el triangulo es equilatero se puede observar que la mediatriz de $MN$ pasa por el circuncentro de $ABC$ (La demostracion es el problema 2 del Estatal de este año) Pero dicho circuncentro esta sobre la bisectriz del angulo en $B$ también, por lo que pertence a la circunferencia circunscrita del triangulo $BMN$ asi el circuncentro de $BMN$ debe estar sobre la mediatriz de $BO$ donde $O$ es el circuncentro de $ABC$ por lo tanto el lugar geometrico que describen es una linea recta (mediatriz de BO).
Saludos
Germán.
jmdEdición
Como se puede observar $BMPN$ es ciclico. De alli que $BMC \equiv CNA$. Entonces $CN=BM$. Y como el triangulo es equilatero, se puede observar que la mediatriz de $MN$ pasa por el circuncentro de $ABC$. (La demostracion es el problema 2 del Estatal de este año.) Pero dicho circuncentro esta sobre la bisectriz del angulo en $B$ también, por lo que pertence a la circunferencia circunscrita del triangulo $BMN$. Asi, el circuncentro de $BMN$ debe estar sobre la mediatriz de $BO$, donde $O$ es el circuncentro de $ABC$. Por lo tanto, el lugar geometrico que describe es una linea recta (mediatriz de BO).
jmdComentario: No se añadieron los acentos (y faltan muchos). Y, bueno, aprovecho para comentar que la buena (o mala) ortografía es una cuestión de actitud: la de valorar el idioma (o no valorarlo). Aprender a escribir bien es entonces un proyecto personal que difícilmente se aprende en el aula. Por otro lado los teclados de las laptops vienen por lo regular en inglés (sin acentos) y eso es un obstáculo que hay que superar (aprender a usarla con comandos vía teclado --una habilidad característica de los expertos en informática).
Te saluda
jmd
Hola Germán. Te hago tres
Gracias Profe Muñoz:) y ahora
Gracias Profe Muñoz:) y ahora que lo pienso tambien me hace falta justificar algo asi como un ''regreso'' . Todo circuncentro de MBN esta sobre la mediatriz, y que todo punto sobre la mediatriz es un circuncentro de MBN, o bueno sobre el segmento que vaya comprender el lugar geometrico.
Senti que era bastante evidente que la mediatriz y la bisectriz se intersectan sobre el circuncirculo, pero bueno la demostracion de este hecho es asi, el punto donde la bisectriz de cualquier angulo en cualquier triangulo, se intersecta con el circuncirculo de dicho triangulo, este punto divide en dos partes iguales al arco comprendido por el lado opuesto de donde parte la bisectriz por lo tanto equidista de los vertices de esta base, y en consecuencia esta sobre su mediatriz.
Ya mañana lo corrigo completo, y trato de subir tambien la solucion del problema 2 de esta Ibero (el de los 9 puntos, ya esta por salir pero....)
Y en cuanto, a la puntuacion, ¿Podria editarla para ver como queda? jaja
Gracias por lo comentarios
Saludos
Germán.