El Cuadrado de Sócrates --y los triángulos notables

Voy a discutir en este post cuatro problemas de geometría básica que se resuelven de manera elemental invocando dos triángulos notables. Estos triángulos son el isósceles rectángulo (la mitad de un cuadrado) y el 30-60-90 (la mitad de un triángulo equilátero). En los dos problemas de inicio, la solución presentada invoca el isósceles rectángulo; en los otros dos se debe invocar la mitad de un equilátero.

Primer problema (el Cuadrado de Sócrates)

Dado el lado $\lambda$ de un cuadrado, construir el cuadrado del doble de área.

Solución

Este es el problema denominado "Cuadrado de Sócrates" (discutido en el Menón). Algebraicamente, debería ser claro que el área del cuadrado de lado $\lambda$ es $\lambda^2$, y el de área doble es el de área $2\lambda^2$. De aquí que su lado debe ser $\sqrt{2}\lambda$. No obstante, con regla y compás, no sería posible construirlo (pues lo que se da es un segmento).

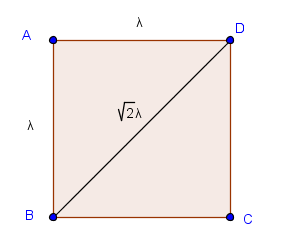
Es por ello necesario apelar a la imagen del cuadrado (de lado $\lambda$) con su diagonal, la cual mide precisamente $\sqrt{2}\lambda$. De aquí que el procedimiento de construcción sea:

• Dibujar el cuadrado de lado $\lambda$;
• trazar su diagonal (una de ellas);
• trazar el cuadrado de lado esa diagonal.

Nota: El método de Sócrates es más fácil y es el siguiente:

• trazar el cuadrado de lado $2\lambda$ (de área $4\lambda^2$);
• los puntos medios de los lados de ese cuadrado forman el cuadrado de área doble

(Se deja como ejercicio para el lector el demostrar que ese cuadrado tiene área $2\lambda^2$.)

Segundo problema (variante del primero)

La diagonal de un cuadrado mide 2 unidades ¿cuánto mide el lado?

Solución

La forma de abordarlo es como en el cuadrado de Sócrates: La diagonal mide raíz de dos por el lado. Pero mide 2. Por tanto, el lado mide $\sqrt{2}$

Tercer problema

La hipotenusa del triángulo $TIN$, rectángulo en $N$, es tangente en $A$ a la circunferencia de centro en $N$ y radio 5. Si el ángulo $INA$ mide 30 grados ¿cuál es el área de $TAN$?

Solución

Primero hay que ver que el triángulo $TAN$ es rectángulo en $A$ (el radio es perpendicular a la tangente). Una vez viendo eso, se debe poder ver que el ángulo en $I$ es de 60 (complementario del dado como dato). Y se puede concluir que los tres triángulos ($TIN,TAN$ y $ANI$) son 30-60-90.

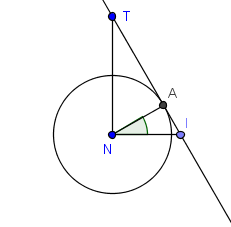
Y, si se tiene clara la imagen de ese triángulo como la mitad de un equilátero, se puede concluir inmediatamente que $TN=10$ (pues el cateto menor vale 5, por dato). De nuevo, de acuerdo a esa imagen, $TA=\sqrt{3}AN=5\sqrt{3}$. Así que el área buscada sea $25\sqrt{3}/2$.

Cuarto problema

El lado $BC$ del triángulo $ABC$ es tangente en $F$ a la circunferencia de centro $A$ y radio 5. Si el ángulo $BAF$ mide 60 y el $ACB$ 15, calcular el área de $ABC$.

Solución

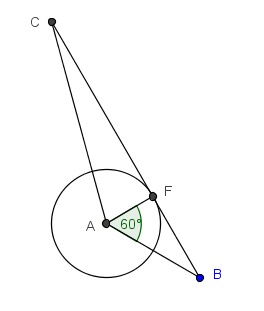
Con la figura es más fácil el razonamiento. Puesto que el radio es perpendicular a la tangente, es fácil concluir que el triángulo $BAF$ es 30-60-90.

Ahora bien, el dato de 15 grados sugiere algo. ¿Qué sugiere? Bueno, sabiendo geometría básica del círculo, ese dato sugiere que se tracen la otra tangente desde $C$ y la otra desde $B$.

Deben intersecarse en un punto (digamos $N$) formando un 30-60-90 con $B$ y $C$. (De aquí tenemos que sacar la longitud de $BC$, la hipotenusa del $BCN$.)

Con lo visto en el problema anterior, debería ser claro (sugiero dibujar el $BCN$ y sus puntos de tangencia con la circunferencia) que $BN=5\sqrt{3}+5$. Pero éste es el cateto menor del $BCN$ (un 30-60-90). Se sigue que $BC=2BN=2[5\sqrt{3}+5]$. De aquí que el área pedida sea $25\sqrt{3}+25$.

 Comentarios finales

Los problemas aquí presentados tratarían de ilustrar la activación (en la mente de un cognizador) de ciertos esquemas muy básicos sobre los triángulos notables. La forma de activarlos es trayendo a presencia sus imágenes después de reconocer a partir de la lectura del enunciado que esos esquemas podrían ser útiles.

De paso, son una invitación a los lectores de MaTeTaM para que se apropien de ellos. Un buen ejercicio en esa dirección es inventar pequeños problemas (como los arriba presentados) con solución basada en los triángulos notables y que sus amigos posiblemente no sabrían resolver.

Claramente, con trigonometría y Pitágoras no es necesario recordar ninguna imagen de ningún triángulo notable... pero en este caso estoy de acuerdo en que la solución creativa es, por decir lo menos, sorprendente.

Los saluda
jmd

PD: Ver http://www.matetam.com/blog/entradas-jmd/trigonometria-examen-enlace-2010 para dos trucos mnemónicos sobre los triángulos notables usados en este post.

PD2: Ver http://www.matetam.com/glosario/teorema/gbc-teorema-del-radio-y-tangente para el resultado de la perpendicularidad del radio y la tangente (los gbc-teoremas de MaTeTaM son básicos, gbc significa "geometría básica del círculo).