El misterioso hechizo del problem solving

En días pasados subí a MaTeTaM todos los problemas de la ONMAS que pude encontrar, y hubo uno que ya había publicado en 2010 y que llamó mi atención pues se ve bastante difícil... y más difícil es la solución que envió Brandon en su momento (basada en una semejanza). 

Bueno, lo difícil es entender la demostración que da de la semejanza --yo no le entendí. El caso es que lo traje en al cabeza varios días, lo resolví de otra manera (por ortocentro) y generé un problema parecido... pero no podía demostrar la semejanza (que parecía obvia en la figura) de una manera alternativa a la que dio Brandon.

Así que en este post voy a abordar ese problema como una forma de olvidarlo... y así liberarme de su hechizo. El problema es el 3 de la X ONMAS 2010 y es 

Un problema hechizante

Sea $ABC$ un triángulo rectángulo con ángulo recto en $B$. Sean $D$ el pie de la altura desde $B, E$ el punto medio de $CD$ y $F$ un punto sobre la recta por $A$ y $B$ de manera que $BA=AF$. Muestra que las rectas $BE$ y $FD$ son perpendiculares.

Solución

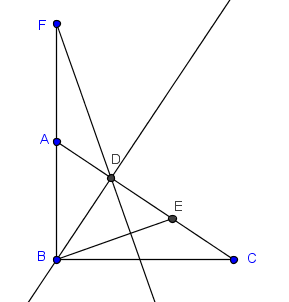
La forma en que lo resolví fue usando una lógica de necesidades. Es decir, visualizando un escenario en el que el problema ya casi estaría resuelto. Por ejemplo, si $D$ fuera ortocentro del triángulo $FBE'$, donde $E'$ es la intersección de $BE$ con la paralela por $F$ a $AC$ --para que $BD$ siga siendo altura. Enseguida se construye tal escenario y se demuestra que sí funciona.

Como nos faltaría la altura de $E'$ respecto al lado $FB$, sería conveniente que $E'D$ fuese tal altura. Ello se lograría si $BCE'D$ fuese paralelogramo --pues en ese caso $E'D$ sería la altura requerida. Una vez visualizado este escenario la solución quedaría así:

Sea $E'$ el reflejo de $B$ respecto al centro $E$ (equivalentemente, $E'$ está en la prolongación de $BE$ de manera que $BE=EE'$). Así que $BCE'D$ es paralelogramo. Pues sus diagonales se bisecan, dado que $E$ es punto medio de $DC$ --por congruencia de triángulos es más largo...

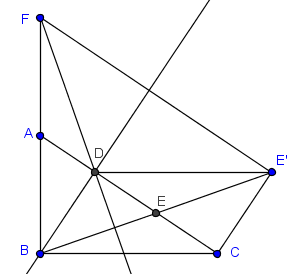
Pero entonces, al ser $E'D//BC$, se tiene que $ED$ es altura de $FBE'$. Y hemos construido un triángulo en el que $D$ es ortocentro. Por tanto, la recta $FD$ es la otra altura (de $F$ respecto a la base $BE'$)--pues las alturas concurren en el ortocentro. Y hemos terminado.

Problema espejo

Sean $ABC$ un triángulo acutángulo y $D$ y $G$ los puntos medios de los lados $AB$ y $BC$, respectivamente. Sean $E$ y $F$, respectivamente, la intersección de la altura de $A$ (respecto al lado $BC$) con la linea media $DG$, y $F$ la intersección de ésta con la perpendicular a $AB$ por $B$. Demostrar que $E$ es ortocentro de $ABC$ si y sólo si $EG=GF$.

Solución

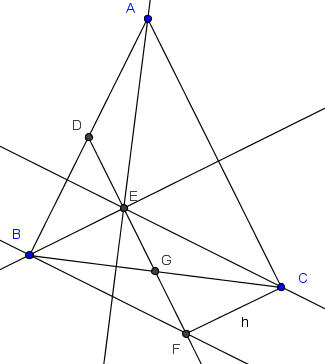
Si $E$ es ortocentro entonces $CE$ es altura (y también $BE$) --pues las alturas concurren en el ortocentro. Así que, por dato, $CE$ es paralela a $FB$. Por tanto, los triángulos $CEG$ y $BFG$ son semejantes. Pero $BG=CG$ ($G$ es punto medio) y se concluye que son congruentes. En consecuencia $EG=GF$.

Si $EG=GF$, entonces $EBFC$ es paralelogramo (sus diagonales se bisecan). De aquí que $EC$ es paralela a $BF$. Pero éste es perpendicular a $AB$ --por dato. Por tanto $CE$ es altura y $E$ es ortocentro.

Sobre la solución de Brandon

Puesto que no le entendía a la demostración de Brandon sobre la semejanza de los triángulos $CEB$ y $BDF$, pero tampoco veía una forma alternativa de demostración, le pedí ayuda a Jesús.

De hecho le pedí que analizara la demostración de Brandon. Pero, en vez de eso, Jesús (después de mirar el problema un rato) me dijo  más o menos lo siguiente: "Se demuestra por el criterio LAL que, por ser poco usado, es el favorito de los diseñadores de problemas; en este caso (que es clásico) uno de los lados del ángulo común se duplica en uno de los triángulos y se reduce a la mitad en el otro."

Y esto último me proporcionó la idea clave. Porque esa idea es convertible en una regla heurística de uso general --con la cual uno puede maliciar la aplicación del criterio LAL y proceder en su consecuencia.

En el caso que nos ocupa, primero habría que conjeturar que $ABD$ es semejante a $BCD$. Esta conjetura también (como en la solución por ortocentro) se derivaría de una lógica de necesidades.

Después de ver que, si fuese cierta, el problema estaría resuelto de la siguiente manera: el suplementario del ángulo $FDB$ (llamémoslo $w$) suma 90 (por dato) con el formado con la recta $FD$ y el lado $DE$; pero el suplementario de $BEC$ mide también $w$ por al semejanza en cuestión --y el resultado se sigue.

Demostración de la semejanza de  $CEB$ y $BDF$

Primero hay que ver que $ABD$ es semejante a $BCD$ (dos triángulos rectángulos formados por la altura $BD$, una configuración clásica). Y, con esa misma configuración es fácil ver que los ángulos $DBA$ y $ECB$ son iguales. (Estos ángulos están formados por los lados cuya proporcionalidad vamos a demostrar.)

Con la semejanza de $ABD$ y $BCD$ ya establecida, planteamos la proporcionalidad en que quedan involucrados los lados de interés: $BD/CD=AB/BC$ o, mejor, $BD/BA=CD/CB$.

Pero, para lo que nos interesa, $CD$ se reduce a la mitad, mientras que $AB$ se duplica (la regla enunciada por Jesús).  Entonces:
$$\frac{BD}{CD/2}=\frac{2AB}{BC}$$
Pero esta proporcionalidad es equivalente a:
$$\frac{BD}{EC}=\frac{FB}{BC}$$
Y se concluye que $CEB$ es semejante a $BDF$ --ya que sus ángulos en $C$ y $B$ tienen medida común y los lados que forman esos ángulos son proporcionales.

Epílogo

Espero que con este post haya cumplido adecuadamente el consejo de la húngara y que su resultado sea el olvido. (De paso, he aprendido una regla heurística del problem solving y generé un problema asociado al dado gracias a mi afán de olvido --lo cual probaría que los efectos de un hechizo no necesariamente son negativos... y, con suerte, pueden llegar a ser muy placenteros.)

Los saluda
jmd

PD: Brandon dice que vio la semejanza mediante una rotación trasladada --eso entendí. Podría ser como sigue --en dos pasos:

PD2: Bueno, creo que en la demostración por ortocentro faltó demostrar que $FE'//AC$. Pero eso es evidente, si observamos que $AE$ es línea media del triángulo $FBE'$...