En este post insisto sobre la idea de que la trigonometría libera al cognizador de la obligación de ser creativo --en situaciones en que ningún trazo auxiliar está a la vista (y menos un procedimiento sintético usando teoremas conocidos).
Ya en otros posts he comentado sobre el uso de la trigonometría en el problem solving de matemáticas de concurso. Ver los siguientes: Trigonometría en ENLACE bachillerato, Trigonometría en ENLACE, y Trigonometría y creatividad.
Ilustraré la tesis con dos problemas de geometría de cierta dificultad (digamos, del nivel de un concurso estatal de olimpiada de matemáticas) --a pesar de que tienen la peculiaridad de parecer elementales.
Primer problema (y un relato)
En estos días llegó a mi cubículo de la universidad un adolescente (Julián) con ganas de triunfar y me planteó el siguiente problema:
Los catetos de un triángulo $ABC$, rectángulo en $A$, miden 60 y 80 unidades y su hipotenusa 100. Un punto $D$ en $BC$ es tal que los triángulos $ABD$ y $CAD$ tienen el mismo perímetro. Calcular $AD$.
Julián había calculado (parece que por tanteos) que $CD=40,DB=60$. "Pero ya no supe cómo seguirle" --me dijo.
Como tengo por política no hacerle la tarea a nadie, primero lo interrogué sobre cómo llegó conmigo (Ramón me lo había mandado) y le planteé algunas preguntas para conocer su nivel de conocimientos.
Me simpatizó que conociera el teorema de Pitágoras y la regla distributiva. (La verdad se la dejé barata, pero en el mundo bizarro de la educación mexicana, el hecho de que un adolescente los conozca lo coloca ya --por ese simple hecho-- en el 5 porciento superior de la curva normal. ) Decidí entonces ayudarle, suspendiendo la exploración de su zona de desarrollo proximal.
El problema tiene la apariencia de ser de secundaria. Con una ecuación o por tanteos se llega rápido a la ubicación de $D$ en la hipotenusa. Este primer avance fácil es desorientador pues, en cierta forma, confirma la hipótesis de ser nivel secundaria.
Pero como nada se me ocurrió para continuar, de repente me sentí como si estuviera en un examen... ("¡¿cómo se juega esto?!" --me dije.)
Me salvó la trigonometría. "Mira, Julián, es claro que $ABD$ es isósceles --¿sabes lo que es eso? Entonces si trazo la altura de $B$... ¿qué tenemos ahí?" Julián me respondió correctamente que sería también mediana, mediatriz, etc.
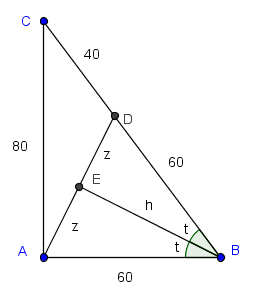
Ello me reconfortó --inútil es buscar la didáctica filosofal cuando el aprendiz no participa del código, ni siquiera en sus rudimentos... Finalmente le dije: "¿sabes trigonometría?" Su respuesta positiva me decidió a mostrarle la siguiente
Solución trigonométrica
Trazamos la altura $h$ de $B$ en el triángulo $ABD$ y denotemos con $E$ su pie en $AD$. Como $ABD$ es isósceles, $AE=ED$ y $\angle{BCE}=\angle{DBE}$.
Denotemos esa distancia con $z$ y a este ángulo con $t$. Tenemos entonces que
$$4/5=\sin{2t}=2\sin{t}\cos{t}=2(z/60)(h/60)$$
Con Pitágoras ($h^2+z^2=60^2$) eliminamos la $h$ y nos queda una ecuación en $z$, la cual resulta bicuadrática (los detalles al lector):
$$z^4-60^2z^2+10^2\cdot{12^4}=0$$
Resolviendo con la fórmula general (o de otra manera), se obtienen las raíces:
$$z=24\sqrt{5}$$
$$z=12\sqrt{5}$$
Así que la solución es
$$2z=24\sqrt{5}$$
Continuación del relato (y la solución creativa)
Después de lograr en el pizarrón esta solución reconstruimos todo el proceso y Julián tuvo la oportunidad de hacer sus preguntas y yo de responderlas --la mayoría fueron de álgebra. Después de agotar las preguntas y las respuestas, le dije: cópiala en tu cuaderno, mientras yo le busco una solución más elemental.
Más elemental, porque la verdad no me la creí que Julián hubiera entendido todo el proceso de la trigonométrica. Pues si bien la trigonometría te ahorra la creatividad de los trazos auxiliares, lo que no sabe ahorrar son las manipulaciones algebraicas.
Todo mundo quizá estaría de acuerdo en que la trigonometría es maquinaria pesada: requiere mucha álgebra (manejo fluido de las manipulaciones algebraicas) y tener disponible en la memoria las identidades y fórmulas trigonométricas.
Entonces me senté en mi escritorio y empecé a escudriñar de nuevo la figura. Y no tardé mucho en ver que trazando dos paralelas aparecen dos configuraciones de Tales (elemental, pero no siempre anda uno crativo). La siguiente es la
Solución creativa
Trazando los segmentos $DE//AB$ y $DF//CA$ aparecen dos configuraciones de Tales. Después de ver eso la solución es obvia. La clave está en que sabiendo la razón en que $D$ divide a la hipotenusa $BC$, se pueden calcular (gracias a Tales) las razones en que $E$ y $F$ dividen a los catetos. Pitágoras vine a dar la puntilla. (Los detalles al lector.)

El otro problema
En este otro problema, yo jugué el papel del aprendiz. Se lo planteé a Jesús Rodríguez Viorato pidiéndole una evaluación experta sobre su dificultad e, indirectamente, una solución alternativa a la que yo tenía --la cual no le mostré sino hasta que él lo resolvió y pudo dar su evaluación.
La solución de Jesús resultó ser trigonométrica --un tanto a su pesar y después de haber buscado una sintética sin encontrarla de inmediato. (El problema tiene la apariencia de ser elemental pero, en realidad, es avanzado.)
Calcular el área de un triángulo $ABC$ sabiendo que su ángulo en $A$ es de 45 grados y, si el pie de la altura de A es $D$, $BD=3$ y $DC=2$
Este problema ya lo tenía yo listo para incluirlo en un post para MaTeTaM pero no había terminado de pulirlo. La idea del post era ilustrar la idea de que una solución sintética (creativa) puede llegar a ser contraintuitiva (en el sentido de que es extremadamente difícil que a alguien se le ocurra).
Solución trigonométrica (editada a partir de la de JRV)

Denotando con $h$ a la altura de $A$, con $s,t$ a los ángulos formados en $A$ por la altura, y con $x,y$ a los lados $AB$ y $AC$, respectivamente (ver figura), las ecuaciones trigonométricas son las siguientes:
$$1/\sqrt{2}=\sin{45}=\sin{(s+t)}=\sin{s}\cos{t}+\cos{s}\sin{t}=\frac{3}{x}\frac{h}{y}+\frac{h}{x}\frac{2}{y}=\frac{5h}{xy}$$
Es decir, $xy/\sqrt{2}=5h$.
Por otro lado,
$$1/\sqrt{2}=\cos{45}=\cos{(s+t)}=\coss\cost-\sins\sint=\frac{h}{x}\frac{h}{y}-\frac{3}{x}\frac{2}{y}$$
Es decir, $xy/\sqrt2=h^2-6$
De estas dos ecuaciones resulta la cuadrática $h^2-5h-6=0$, la cual tiene las raíces $h=-1$ y $h=6$. De aquí que el área pedida sea de 15 unidades cuadradas.
Solución creativa
Puesto que ya tenemos la base ($BC=5$), el problema quedaría resuelto si supiéramos la altura de $A$ desde $BC$. ¿Es $AD$ calculable de los datos? No parece pero... El problema es interesante precisamente por esta aparente imposibilidad.
En la siguiente figura se puede inferir un procedimiento para la construcción del triángulo descrito en el enunciado: dibujar la base $BC$ y el punto $D$ de manera que la divida en razón 3/2; trazar el isósceles $BCE$, rectángulo en $B$; trazar el circuncírculo de $BCE$; $A$ se localiza en el circuncírculo y en la perpendicular por $D$ a $BC$.

Este procedimiento de construcción es en sí mismo la solución de un problema:
Dibujar, con regla y compás, un triángulo $ABC$ dado que: su ángulo en $A$ es de 45 grados; el pie $D$ de la altura de A divide a la base $BC$ en razón 3/2 ($BD=3$ y $DC=2$).
Volviendo a considerar la figura, es posible descubrir el cuadrilátero cíclico $AEBC$. Y, con ello, se descubre también que $EA$ es perpendicular al lado $CA$... y posiblemente la siguiente cadena de inferencias ($H$ es el ortocentro de $ABC$):
- $AEBH$ es paralelogramo;
- de aquí que $AH=5$;
- y el área $(ABC)$ del triángulo $ABC$ sería $5(5+HD)$.
Ahora el problema se reduce a encontrar $HD$. ¿Ningún avance? Bueno, terqueandole otro rato debería llegar la idea de usar potencia de un punto (el punto $D$) para establecer una ecuación.
Pero esta idea debería también traer a presencia el teorema que asegura que el ortocentro $H$ reflejado en el lado tiene su imagen $H'$ en el circuncírculo. La ecuación resultante es $2\cdot3=h\cdot{HD}$.
Ahora recordemos que ya expresamos la altura en términos de $HD$. Denotando a $HD$ con $z$, la ecuación que resuelve el problema es una cuadrática:
$$6=(5+z)z$$
$$z^2+5z-6=0$$
$$(z-1)(z+6)=0$$
Por tanto, $HB=1$ y la altura buscada es 6. La respuesta es entonces: el área del triángulo $ABC$ es 15 ($=5\times{6}/2$).
Comentarios finales
En ambos problemas se dan datos concretos sobre longitudes de segmentos y ello es una trampa cognitiva: conduce a concluir que el problema es elemental. No obstante, una solución elemental no es fácil de lograr.
En el primer problema, la solución creativa tiene que pasar por ver que trazando ciertas paralelas el problema se reduce a una aplicación de Tales y Pitágoras. La dificultad estriba en descubrir esos trazos, es decir, en poner el problema en un marco adecuado.
El plan B de solución fue recurrir a la trigonometría (después de ver el isósceles y trazar su altura, el plan trigonométrico es bastante natural).
En el segundo problema, la solución creativa requiere demasiados conocimientos combinados: trazar perpendicular a $BC$, ver un cíclico, ver un paralelogramo, decidir usar potencia de un punto, apelar al teorema de la reflexión del ortocentro,...
Los datos en el problema no dan ninguna sugerencia, ninguna invitación a seguir este largo y sinuoso camino.
La solución trigonométrica del segundo problema (al igual que la del primero) queda sugerida por la figura inicial --y no exige ningún trazo adicional (el problema se resuelve sin hacer ningún trazo).
Isn´t it good, trigonometry mood?
Los saluda
jmd
PD: si alguien tiene otras soluciones lo invitamos a compartirlas...

Tengo ya dos soluciones para
Tengo ya dos soluciones para el segundo problema. Aunque también utilizan manipulación trigonométrica.
Primera solución (completamente trigonométrica):
Utilizando la primera figura mostrada en el enunciado de este problema, tenemos que $tan(t)=\frac{2}{AD}$ y $tan(s)=\frac{3}{AD}$. Debido a ello tenemos que $tan(s)=\frac{3tan(t)}{2}$ ....................... $(1)$.
Luego por la identidad:
$tan(x+y)=\frac{tan(x)+tan(y)}{1-tan(x)tan(y)}$ pasamos a sustituir para $t,s$, tomando en cuenta $(1)$
$tan(s+t)=tan(45)=1=\frac{tan(t) + \frac{3tan(t)}{2}}{1 - tan(t) - \frac{3tan(t)}{2}}$
O lo que es lo mismo, $1=\frac{5tan(t)}{2-3tan^{2}(t)}$ para así obtener la ecuación de segundo grado: $3tan^{2}(t) + 5tan(t) - 2 = 0$, con soluciones $tan_{1}(t)=-2$ y $tan_{2}(t)=\frac{1}{3}$. Debido a que $tan(t)=\frac{2}{AD}$ descartamos la primer solución (es decir, $tan_{1}(t)$). De este modo, tenemos que $tan(t)=\frac{1}{3}$. A esta conclusión la denominaremos $\alpha$.
Con este resultado tenemos finalmente que $AD=\frac{2}{tan(t)}=\frac{2}{\frac{1}{3}}=6$, y así el área nos resultará $(ABC)=\frac{AD\cdotBC}{2}=\frac{6\cdot5}{2}=15$.
Segunda solución:
Sean $P$ el pie de la altura trazada desde $B$ y $H$ el ortocentro del triángulo $ABC$. Tenemos que $s+t=45°$ por lo que en el triángulo $ABP$, el ángulo $\angle{APB}=45°$, lo que nos arroja, aparte de que $BPA$ es isósceles, que $\angle{PCH}=45°$ (debido a los ángulos formados al trazar las tres alturas, por este argumento también decimos que $\angle{HBD}=t$ y $\angle{HCD}=s$). Por lo tanto, el triángulo $HPC$ también es isósceles, con $HP=PC$.
Ahora tenemos la semejanza de triángulos $BPC \sim APH$ (por AA), cumpliendo las razones $\frac{BP}{AP}=\frac{PC}{PH}=\frac{BC}{AH}=1$ (debido a que $HP=PC$). Con esto, obtenemos que $AH=BC=5$.
Es momento de utilizar la parte trigonométrica, por el argumento $\alpha$ de la solución anterior, tenemos que $tan(t)=\frac{1}{3}$ y por el triángulo $BHD$, sabemos que $tan(t)=\frac{HD}{3}$, uniendo estos últimos dos argumentos, obtenemos que $HD=1$. Así tenemos finalmente que $AD=AH+HD=5+1=6$ y que el área del triángulo $ABC$ es $15$.
Un saludo.
Yo veo muy bien las dos
Yo veo muy bien las dos soluciones. Fíjate que me gustó más la primera, no lo había pensado, pero es más natural estudiar las tangentes si lo que uno quiere es calcular la altura del triángulo.
En la parte de la segunda
En la parte de la segunda solución donde dices: "Es momento de utilizar la parte trigonométrica..." yo lo podría ver aun de manera geométrica haciendo semejanza de los triángulos HDC y BDA:
HD / BD = DC / DA y como ya tenemos que AH=5, BD=3 y DC=2 asi:
(HD) / (3) = (2) / (5+HD)
entonces: (HD)² + 5(HD) = 6 luego: (HD)² + 5(HD) - 6 = 0 (HD+6)(HD-1) = 0 ==> HD = 1
AH = 6 y BC = 5, entonces el área es 15.
Pues con eso se completa la
Pues con eso se completa la idea de de Daniel, de hacer una demostración sin trigonometría. Muy buena observación. Gracias
Prácticamente la segunda
Prácticamente la segunda solución es otra forma (evidentemente más complicada, pero que existe debido al capricho personal de utilizar construcciones) de terminar la primera solución.
Gracias por la colaboración
Gracias por la colaboración Daniel. Te comparto las siguientes soluciones (como curiosidad de postproducción):
Con la tangente de la suma de ángulos (como tú lo haces, pero calculando directamente a partir de los datos las tangentes), el problema del área sale en tres patadas (después de haberlo traído en la cabeza todo un día...)
Efectivamente, el problema del área se reduce a calcular la altura $h$ de $A$. Pero $h=AD$ se puede calcular con la tangente de la suma de ángulos: