Este post, al igual que el anterior, se inscribe en la Reforma al Bachillerato (Bloque I, Matemáticas II). En él voy a elaborar (discutir) sobre los procesos de inferencia que pueden realizarse en configuraciones geométricas muy básicas, utilizando el concepto de ángulos congruentes. Y algunos resultados muy básicos, como el de la suma de los ángulos interiores de un triángulo, las relaciones de complementariedad y suplementariedad de dos ángulos.
Para ello inicio con la definición de la relación de congruencia de ángulos en términos de un experimento imaginario (la superposición de un ángulo sobre otro) por considerar (al estilo euclidiano) que la congruencia es anterior a la medida. Después se define el triángulo isósceles y se "demuestra" que, en un isósceles, sus ángulos en la base son congruentes.La "demostración" se realiza mediante el experimento imaginario de la superposición.
(Como se sabe, Euclides define las rectas perpendiculares como aquéllas que forman en su intersección ángulos congruentes. Y aunque ese espíritu se ha perdido en los textos escolares, me parece que la congruencia de ángulos es anterior a toda medición de los ángulos. Una vez que se ha establecido una unidad de medida de los ángulos, ya se puede decir "se cortan a 90 grados" o "forman un ángulo de $\pi/2$")
Una vez contando con la herramienta (el teorema) del triángulo isósceles, por lo demás muy básica, se demuestra el teorema del ángulo inscrito en una semicircunferencia. Este ejercicio --y los restantes del post-- estaría orientado a practicar los procesos de inferencia propios del problem solving en geometría. Pero también conduce a una primera construcción geómetrica (levantar una perpendicular) y a otras construcciones después de tener otras herramientas disponibles.
A partir de aquí, se plantea como algo natural el ver la hipotenusa como diámetro de la circunferencia que pasa por los vértices del triángulo rectángulo. (Equivalentemente: el punto medio de la hipotenusa es equidistante de los vértices del triángulo rectángulo.)
Tratando de extraer todo su potencial a la congruencia de triángulos, se inicia una discusión de las propiedades de un rombo, para regresar de nuevo hacia la mitad del post, al triángulo isósceles: la bisectriz del ángulo opuesto a la base de un isósceles es también mediatriz, altura, mediana.
De este hecho se derivan dos construcciones geométricas: trazar bisectriz de un ángulo y trazar mediatriz de un segmento. La hebra que pude extraer de la congruencia de dos triángulos llegó hasta la discusión de los triángulos notables y el teorema de Pitágoras.
Teorema del triángulo isósceles
Ángulos congruentes: Dos ángulos se dicen congruentes si al superponerlos coinciden.
Triángulo isósceles: Se dice que un triángulo es isósceles si tiene dos lados iguales. (Nota: se acostumbra llamar base de un isósceles al tercer lado, después de los dos iguales.)
Teorema del triángulo isósceles: Los ángulos en la base de un triángulo isósceles son congruentes.
Demostración (visual y experimental)
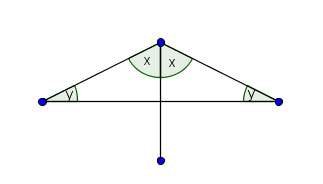
El siguiente experimento imaginario se puede realizar físicamente, si el aprendiz lo desea. Sea $ABC$ el isósceles con $AB=AC$ y base $BC$. Ahora imaginemos que tenemos dos copias exactas uno del otro y que los hacemos coincidir.
Primero observemos que tienen que coincidir pues uno es la copia del otro. Pero también coinciden si nos equivocamos, y en el vértice $B$ del original colocamos el $C$ de la copia y en el $C$ del original el $B$ de la copia. Se concluye que el ángulo $ABC$ es congruente con el $ACB$. Es decir, los ángulos en la base de un isósceles son congruentes.
El otro teorema de Tales
Teorema del ángulo en semi-circunferencia: Todo ángulo inscrito en la mitad de una circunferencia es recto.
Sea AB el diámetro, O el centro, y P un punto en la semi-circunferencia.

Puesto que $OP,OB,OA$ son radios, tenemos los isósceles $OPA, OPB.$

Llamemos $x$ a los ángulos en la base $PA$ del triángilo $OPA$ y $y$ a los ángulos en la base del $OPB.$ Queremos demostrar que el ángulo $APO$ es recto. Para ello usaremos el hecho de que la suma de los ángulos interiores de un triángulo es 180.

Sumando los ángulos del triángulo $ABP$ se obtiene $2x+2y=180.$ De aquí que $x+y=90.$ Como se quería.
Instancia de uso (levantar una perpendicular)
Por un punto dado $P$ de una recta dada $l$ trazar una perpendicular.
Procedimiento de construcción:
1. Marcar un punto $O$ cualquiera fuera de la recta $l$.
2. Trazar un círculo con centro en $O$ y radio $OP$, y marcar la otra intersección del círculo con $l$, llamémosla $Q$.
3. Trazar el segmento $QO$, y prolongarlo hasta que corte al círculo en $P'$.
4. La recta $P'P$ es la perpendicular buscada.
Dos ejercicios de deducción:
- La hipotenusa de un triángulo rectángulo es el diámetro de la circunferencia que pasa por sus vértices. Ejercicio: comprobarlo.
- El punto medio de la hipotenusa es equidistante de los tres vértices del triángulo rectángulo. Ejercicio: demostrarlo.
Rectas notables del triángulo
Altura (de un vértice respecto a un lado): es el segmento que va del vértice a su lado opuesto y es perpendicular a éste.

Bisectriz de un ángulo: Es la recta que pasa por el vértice y que divide al ángulo en dos ángulos congruentes.
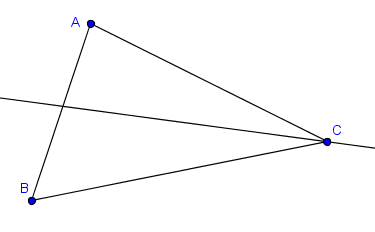
Mediana: es el segmento que va del punto medio de un lado al vértice opuesto.
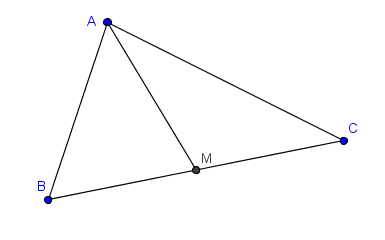
Mediatriz de un segmento: es la recta perpendicular al segmento por el punto medio de éste.

Rombo
El rombo es un cuadrilátero con sus 4 lados congruentes.

Al trazar en el rombo cualquiera de sus diagonales se forman dos triángulos isósceles, uno a cada lado de la diagonal. Aprovecharemos este hecho para demostrar algunas propiedades del rombo.
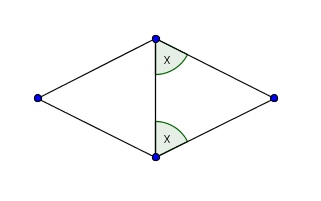
Tracemos una diagonal y focalicemos los isósceles que se forman. Llamemos $x$ a la medida de los ángulos en la base de uno de los isósceles.
Ahora tracemos la otra diagonal y focalicemos los isósceles a sus lados. Llamemos $y$ a los ángulos en la base de uno de los isósceles recién formados.
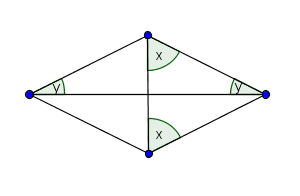
Pero necesitamos aplicar suma de ángulos. Por tanto terminemos de nombrar los ángulos restantes.

Ahora sí podemos aplicar suma de ángulos. Para el triángulo izquierdo se tiene la ecuación $2w+y+z=180$. Para el derecho se tiene la ecuación $2x+y+z=180.$
De aquí que $w=x$ (igualando y cancelando).
Pero si $w=x$, entonces se tiene que, en el triángulo superior, $2x+2y=180.$ De donde se obtiene que $x+y=90.$ Se concluye que las diagonales de un rombo son perpendiculares (pues el ángulo en su intersección es suplementario de $x+y$, y como esta suma es 90...)

Por otro lado, sumando los ángulos en el triángulo inferior, se tiene que $2x+2z=180$, es decir, $x+z=90$. De aquí que $z=y$ (pues $z$ y $y$ son complementarios del mismo ángulo $x$). Se concluye que las diagonales son bisectrices de sus ángulos que dividen en dos.
Finalmente, observando que cada diagonal divide al rombo en dos triángulos que son copias uno del otro, podemos imaginar (o realizar) el siguiente experimento: recortando (o doblando) sobre una de las diagonales del rombo, los dos triángulos resultantes coinciden al superponerlos el uno sobre el otro.
Se sigue que la otra diagonal quedó cortada por la mitad exacta (por su punto medio). Por tanto las diagonales de un rombo son mediatrices una de la otra (se bisecan perpendicularmente).
Si ahora consideramos solamente uno de los triángulos isósceles, digamos el superior, entonces hemos llegado a que la bisectriz del ángulo opuesto a la base de un triángulo isósceles es también altura (perpendicular del vértice a la base), mediatriz (perpendicular por el punto medio de la base) y mediana (une el punto medio de la base con el vértice opuesto).

Construcciones geométricas derivadas del rombo
Construcción de la bisectriz de un ángulo
Dado un ángulo, trazar su bisectriz con regla y compás.
Procedimiento de construcción
1. Con centro en el vértice V y una abertura cualquiera marcar los puntos P y Q sobre los lados.
2. Con la misma abertura y haciendo centro primero en P y luego en Q trazar dos arcos de manera que se crucen (digamos en V')
3. La recta VV' es la bisectriz del ángulo dado.
Construcción de la mediatriz de un segmento AB
Dado un segmento, trazar su mediatriz con regla y compás.
Procedimiento de construcción
1. Con una abertura cualquiera y haciendo centro en AQ trazar un círculo.
2. Con la misma abertura y haciendo centro en B trazar un círculo.
3. La recta que pasa por las dos intersecciones (digamos P y Q) de los círculos es la mediatriz del segmento AB.
Nótese que, por construcción, el cuadrilátero APBQ es un rombo. Nótese también que el mismo procedimiento ubica el punto medio del segmento $AB$.
Bajar una perpendicular
Trazar una perpendicular a una recta $l$, por un punto P fuera de ella.
Procedimiento de construcción
1. Marcar un punto $Q$ sobre la recta $l$
2. Marcar el punto medio $O$ del segmento $PQ$
3. Dibujar la ciercunferencia de centro $O$ y radio $OP$
4. Si $P'$ (distinto de $Q$) es la otra intersección de la circunferencia con $l$, entonces $PP'$ es la perpendicular buscada.
Triángulos notables o típicos
Triángulo equilátero
El triángulo equilátero se define como aquél que tiene todos sus lados iguales (congruentes).
Consideremos el triángulo equilátero $ABC.$ Si elegimos $BC$ como su base, tenemos que $AB=AC.$ Entonces sus ángulos en la base son congruentes (iguales). Llamémosles $x.$
Si ahora elegimos como base $AB$, tenemos que $CA=CB$. Entonces sus ángulos en la base $AB$ son congruentes (iguales) --por el teorema del triángulo isósceles. Pero el ángulo en $B$ mide $x$. Por tanto el ángulo en $A$ mide también $x.$ Se concluye que un triángulo equilátero es también equiángulo.
Pero, además, por suma de ángulos interiores, se tiene que $x+x+x=180.$ Por tanto $x=60$. Es decir, los ángulos de un triángulo equilátero miden 60 grados.
Triángulo rectángulo 30, 60, 90 (mitad de un equilátero)
Si trazamos la bisectriz de un equilátero, sabemos que es también mediatriz. Por tanto,
la mitad de un equilátero es un triángulo rectángulo cuyos ángulos son de 30, 60 y 90.
Si imaginamos que el lado del equilátero mide $2k$ unidades, entonces
el triángulo rectángulo 30, 60, 90 tiene la propiedad de que el cateto menor mide la mitad de su hipotenusa (mide $k$ unidades).
Triángulo rectángulo isósceles (mitad de un cuadrado)
Un cuadrado es un rombo con todos sus ángulos congruentes. Consideremos un cuadrado de lado $k$. Tracemos una de sus diagonales. Entonces la diagonal divide al cuadrado en dos triángulos rectángulos isósceles.
Por el teorema del triángulo isósceles, sus ángulos en la base son iguales (congruentes). Pero como es triángulo rectángulo, por suma de ángulos interiores, se concluye que los ángulos en la base de un triángulo rectángulo isósceles miden 45 grados.
Teorema de Pitágoras
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Consideremos la figura siguiente que consiste de dos triángulos rectángulos que son copia uno del otro, acomodados de tal manera que el cateto menor de uno está alineado con el cateto mayor del otro.
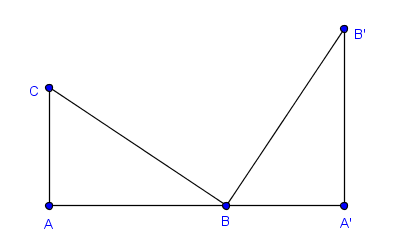
a) Calcula la medida del ángulo $B'BC$ en términos de las medidas $y, z$ de los ángulos no rectos del triángulo original.

b) Cerrando el trapecio como se muestra en la figura, calcula su área en términos de las longitudes de los catetos.
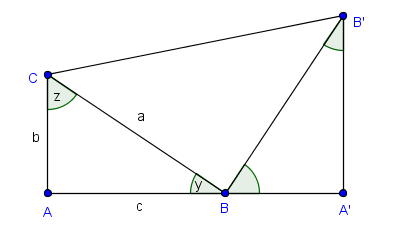
c) Calcula el área del trapecio de otra manera y plantea una ecuación, para demostrar el teorema de Pitágoras.
Los saluda
jmd
