Blogs
Sobre el problema 3 del selectivo final
El problema y la solución de Germán
Cuadrilátero cíclico: más instancias de uso
En este post voy a recomendar el estudio de algunos materiales sobre cuadriláteros cíclicos a quienes se están preparando para el nacional. De paso intercalo dos instancias de su uso.
En un post anterior --dedicado a los criterios de reconocimiento de los cuadriláteros cíclicos-- hemos destacado la importancia de esta herramienta en el problem solving de geometría y discutimos varias instancias de uso asociadas a demostraciones del teorema de la mariposa.
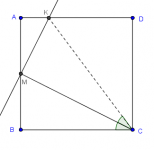
Selectivo 2 OMM_Tam_2014
Enseguida presento los cuatro problemas del segundo examen selectivo para la preselección Tamaulipas OMM 2014. Añado las soluciones al 2 y al 4.
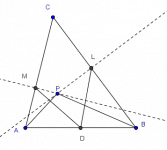
Problema 1. En un cuadrilátero ABCD convexo se trazan las perpendiculares desde cada vértice a la diagonal que no pasa por él. Demostrar que los cuatro puntos de intersección de cada perpendicular con su correspondiente diagonal forman un cuadrilátero semejante al dado.
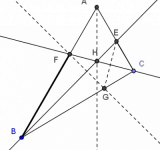
Primos y divisibilidad: dos problemas
Voy a comentar en este post las soluciones de los problemas 1 y 2 del primer selectivo para la preselección OMM Tamaulipas 2014. Espero que sirva como feedback para los preseleccionados que no los resolvieron o los resolvieron de otra forma. (Vaya una felicitación para Camilo por su excelente elección de los problemas.)
Problema 1. Sean m,n enteros positivos tales que $m^2+n^2$ es múltiplo de 3. Pruebe que m y n son también múltiplos de 3.
Comentario:
Héctor R. Flores C.: una didáctica del reconocimiento
Cuadrilátero cíclico --criterios e instancias de uso
Puesto que el material disponible en la Web sobre los cuadriláteros cíclicos no incluye las demostraciones de los criterios de su reconocimiento (con excepciones difíciles de encontrar) voy a presentar en este post los tres criterios para el reconocimiento de un cuadrilátero cíclico, así como sus demostraciones. Añado tres instancias de uso.
Definición y criterios de reconocimiento
Primero la definición:
Si los cuatro vértices de un cuadrilátero convexo están sobre la misma circunferencia, entonces se dice que el cuadrilátero es cíclico.
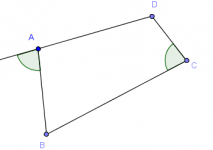
Pensamiento lateral (¡¿Alguien me puede explicar eso?!)
Me he encontrado en estos días con el tema del pensamiento lateral y, sobre todo, con sus acertijos. Y creo que puede ser de alguna utilidad para los lectores de MaTeTaM una discusión sobre esos acertijos y su relación con los chistes y los problemas de matemáticas de concurso. La clave que los une es la interpretación de unos datos desde un cierto punto de vista.
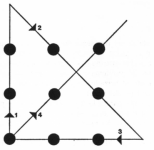
El difícil de la ONMAPS --Tamaulipas 2014
Concurso Municipal OMM Tamaulipas 2014
Hoy 4 de abril de 2014 se aplicó el examen del concurso municipal, primera etapa del proceso de selección de la Olimpíada Mexicana de Matemáticas en Tamaulipas. Pongo en este post los problemas con sus soluciones (algo condensadas) como una retroalimentación para los participantes.
1. En un examen de 10 preguntas, Juan las respondió todas y obtuvo 29 puntos. Si le dieron 5 puntos por cada respuesta correcta y -2 por cada incorrecta ¿cuántas preguntas respondió Juan correctamente?
Solución
El modelo algebraico es: x+y=10, 5x-2y=29. La respuesta es x=7.
El difícil de la olimpiada de la SET (Jugando con las Matemáticas)
Ocho albañiles construyen una barda de 30 metros en 9 días trabajando 6 horas diarias. ¿Cuántos días tardarán 10 obreros para construir 50 metros de barda trabajando 8 horas diarias?
Este problema fue el último (el 5) del examen estatal de la olimpiada para tercero de secundaria celebrada el 26 de marzo en Cd Victoria Tamaulipas. Ninguno de los tres concursantes lo resolvió. ¿En qué consiste su dificultad? Voy a comentar en este post la solución y a compararlo con un problema clásico de proporcionalidad inversa.
