Blogs
Sobre el difícil del estatal OMM Tamaulipas 2013
En el concurso estatal de la XXVII OMM Tamaulipas 2013, el problema 4 fue de álgebra y la expectativa era que nadie lo resolvería. Pero, para nuestra sorpresa, un alumno del CBtis 15 (el plantel sede) lo resolvió correctamente (usando derivadas). Vaya una felicitación para Oscar Rosas Castillo por no dejarse intimidar por ese problema --y por tener las herramientas necesarias para resolverlo.
El problema (y algunos comentarios)
4A. Encontrar el valor mínimo de la expresión $(x^4+x^2+5)/(x^2+1)^2$ y el valor de la $x$ para el cual se logra.
Problem solving con vectores
En este post voy a argumentar a favor del uso de los vectores en el problem solving en geometría. Con las definiciones iniciales de vector, vectores de posición, vectores libres, igualdad de vectores, y la suma y resta de vectores presento la demostración de varios teoremas de la geometría como instancias de uso de esta poderosa herramienta. Destacan las instancias de uso finales sobre la demostración puramente vectorial de la fórmula de Sylvester y de la Recta de Euler.

Julio Antonio Serrano De los Santos: un estilo mutante de administrar
Como se sabe, el significado básico de mutación es cambio (mutar, mudar). Y, en genética, es una alteración en la información genética de un ser vivo que cambia las características de éste (respecto a las usuales mostradas por los individuos de su especie) y que es incorporable a los mecanismos de la herencia.
Desde la perspectiva de la teoría evolutiva, el mutante introduce la variedad en una población y, por tanto, la posibilidad de un cambio en ella. Es decir, la posibilidad de evolucionar.

Entrenamiento en Olimpiada --de Orlando Ochoa
Orlando Ochoa Castillo generosamente ha enviado a la Delegación Tamaulipas de la OMM el contenido de los entrenamientos de la selección Guanajuato. No los había puesto en MaTeTaM porque no sabía cómo --dado que están en formato PDF.
Los comparto ahora con los lectores de MaTeTaM (como es la intención expresa de Orlando) para que estén disponibles en la Web para quien quiera seguirlos por su cuenta y, en particular, para los (futuros) preseleccionados de Tamaulipas --para la segunda semana de octubre se definirán. El material --que incluyo en los atachados-- consiste de nueve sesiones y algunas tareas.
Un problema de geometría --de Wong Yan Loi
En su libro Introduction to geometry, Wong Yan Loi presenta el problema motivo de este post (y lo resuelve con geometría analítica). La redacción del enunciado está aquí ligeramente modificada y a la solución le he añadido explicaciones que Wong Yan Loi se ahorra. (Me gustaría ver una solución sintética de este problema. Si alguien la encuentra sería una buena obra que la compartiera con los lectores de MaTeTaM.)
El 5 del VI concurso nacional OMM 1992
Cuando llueve, como en estos días que se formó en el Golfo de México la tormenta Ingrid, me pongo inspirado y con ganas de postear. Buscando qué hacer mientras llovía me encontré con este problema del concurso nacional de 1992 (VI OMM).
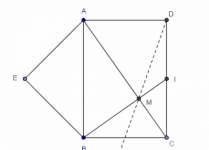
Teorema fundamental de la proporcionalidad (Tales)
Si una recta paralela al lado $BC$ del triángulo $ABC$ corta en $B'$ a $AB$ y en $C'$ a $AC$), entonces $$\frac{AB}{AB'}=\frac{AC}{AC'}=\frac{BC}{B'C'}$$
Este es el Teorema de Tales para triángulos del cual hemos hablado ya en MaTeTaM. En esta oportunidad comentaré el teorema particularizado para triángulos rectángulos y lo demostraré con el método de áreas.
Método Singapur --para razonar problemas verbales elementales
Llamo problemas verbales (word problems) a los problemas razonados con los que se introduce (o debería introducirse) el razonamiento matemático en la escuela primaria (en quinto y sexto año por lo menos). Voy a ilustrar el tema con
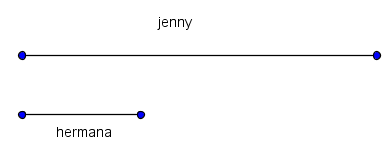
Un ejemplo
Jenny tiene 7 pesos y su hermana 2. Después de que su madre les da una misma cantidad de pesos Jenny tiene el doble que su hermana. ¿Cuánto recibieron de su madre?
Solución algebraica
El fácil del concurso XV OMM (2001)
Con motivo del comentario-solución de Germán Puga Castillo al problema 1 del concurso nacional de la OMM 2001 (y el feedback de Jesús Rodríguez Viorato), el problema llamó mi atención por su aparente simplicidad. Voy a comentarlo en este post (y a resolverlo apoyándome en la idea de Germán). El problema es el siguiente:
Encuentra todos los números de 7 dígitos que son múltiplos de 3 y de 7, y cada uno de cuyos dígitos es 3 o 7.
Dos problemas razonados --para segundo de secundaria
En este post voy a discutir dos problemas razonados que, según la reforma de secundarias 2011, los alumnos que pasan a tercer año deberían estar en posibilidad de resolverlos. Su modelación conduce a un sistema $2\times2$ (dos ecuaciones, dos incógnitas).
Idealmente están al alcance de un adolescente de 14, pues en el bloque V del programa de matemáticas de segundo de secundaria, uno de los aprendizajes esperados es:
Resuelve problemas que implican el uso de sistemas de dos ecuaciones lineales con dos incógnitas.
