Blogs
Jornada 2. Actividad para Preselección Tamaulipas 2016
Actividad de Verano para Preselección Tamaulipas 2016 (Jornada 1)
El día de hoy comenzamos con las actividades para la preparación de la Preselección Tamaulipas 2016 en el receso de verano.
Para esto diseñamos un juego al estilo de las Ligas Fantásticas deportivas que hay para varios deportes. Adjunto el archivo con las reglas del juego.
Cada semana serán equipos distintos, y podríamos ajustar algunas reglas para hacer más interesante la actividad. Semana a semana se irá actualizando el ranking de la puntuación obtenida por cada alumno.
Examen de prueba para el estatal
Que mejor manera de prepararse que un examen para calentar, pueden intentar hacerlo lo más parecido a un examen normal, es decir separan 4 horas de su tiempo y lo intentan resolver en ese lapso. De cualquier manera, es importante que los resuelvan. Tal vez subamos las soluciones en próximos días.
Saludos
germán
Soluciones.
Problema 1: Primero hay que responer la pregunta: ¿De cuántas maneras puedes expresar un entero n como suma de tres números sin que el primero sea cero?
Prepárate para el Estatal con MaTeTaM (Combinatoria)
Para finalizar esta serie de post me gustaría dar algunos temas para el área de combinatoria.
Técnicas de conteo: Principio aditivo y múltiplicativo, definición de factorial, combinaciones con y sin repetición, conteo con restricciones, y técnicas de conteo como contar por complementos, por casos, recursión etc.
También es conveniente tener un razonamiento a partir de modelos básicos en combinatoria como distribución de pelotas en cajas, lanzamientos de dados, recorridos en cuadrículas, dinámicas con cartas o barajas etc.
Prepárate para el Estatal con MaTeTaM (Geometria)
Siguiendo con esta serie de posts dejaré los temas importantes para el estatal, en este caso para geometria. También una lista de problemas (listageometria2016) y algunos entrenamientos, se da por sentado el tema de áreas, la lista incluye unos pocos problemas de esto pero son retadores.
No es cien por ciento necesario que aprendan a hacer demostraciones aún pero algunos problemas de geometria solo se pueden aprender si se conocen las demostraciones de algunos resultados y en que instancias se usan.
1. Ángulos entre paralelas. Hacer problemas del entrenamiento adjunto.
Carta de Agradecimiento
Con el examen de la Etapa Regional han finalizado las fases en ciudades de la Olimpiada de Matemáticas en Tamaulipas. En días anteriores estuve un poco desconectado porque acompañé a los alumnos que participaron en la ONMAPS en la Ciudad de México, y por lo tanto no había tenido oportunidad de agradecer a todos los que nos han dado este gran apoyo en sus escuelas y municipios.
Prepárate para el Estatal con MaTeTaM (Números)
Para mejorar el desempeño de los competidores tamaulipecos en el Estatal, hemos decidido hacer una serie de posts compartiendo lo necesario para competir el 1 de julio. Esta primera entrada va orientada a aritmética o teoría de números, los temas necesarios son:
Sistema Decimal. Este tipo de problemas son ateoricos pues no se necesita saber mucho, son casi de lógica con un poco de combinatoria. No por eso son los más sencillos. Para participar en la olimpiada no necesitas saber más que los demás, si no saber usar lo que sabes.
Prepárate para el municipal
Como saben, este Viernes 20 de Mayo será la primera etapa en nuestro proceso 2016.
El delegado Orlando ha enviado un examen de prueba para los que quieran conocer que tipo de problemas aparecerán el Viernes, al final lo adjunto.
También aprovecho para recordarles que aún se pueden inscribir para el concurso, llenando el formulario que se encuentra en el siguiente link:
https://docs.google.com/forms/d/1pi8UPeCY2HguynVcoHPfBi_jnmC1UTYvC-ojMYRWjNw/viewform?c=0&w=1
Los esperamos este Viernes :)
Saludos
germán
Jornadas en la Olimpiada de Tamaulipas
Para calentar motores antes de que inicie el proceso 2016, hemos (Orlando Ochoa, José Luis Medellin, Luis Javier Olvera,Roberto Alain y un servidor) diseñado un nuevo formato de competencia para los alumnos tamaulipecos que pueden volver a participar este año. Las llamadas ''Jornadas'' es una lista de problemas, que los alumnos realizan por equipos, y se evaluan dandoles puntos extras además de los 7 puntos por la solución de los problemas. Cada semana hay ganadores y una tabla de posiciones. La explicación del formato tal vez sea para después. Después de tres Jornadas, los problemas y soluciones más interesantes son los siguientes:
Jornada 1
Sobre el problema 1 de la 29 OMM
El problema
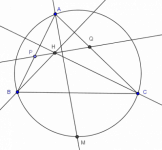
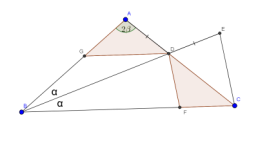
Sea $ABC$ un triángulo y sea $H$ su ortocentro. Sea $PQ$ un segmento que pasa por $H$ con $P$ en $AB$, $Q$ en $AC$ y tal que $\angle PHB=\angle CHQ$. Finalmente en el ciruncírculo del triángulo $ABC$ considera $M$ el punto medio del arco $BC$ que no contiene a $A$. Muestra que $MP=MQ$.
La solución
De acuerdo a los datos sobre la recta PQ que pasa por H, es fácil darse cuenta que PQ es bisectriz de los ángulos formados en H por las alturas.