Noticias
Preselección OMM Tamaulipas 2012
He aquí la lista de la preselección OMM Tamaulipas 2012 (tal y como me la envió el delegado Ramón Jardiel Llanos Portales --así que cualquier aclaración, felicitación o incluso impugnación, sea ésta con pruebas o sin pruebas, por favor comunicarla directamente a rjardiel5@hotmail.com ).
|
GABRIELA SAC-NITE GUEVARA MTZ |
OMM Tamaulipas 2012: concurso estatal
El día de hoy, 5 de octubre, se aplicó el concurso estatal en las instalaciones de la UAMCEH-UAT, de donde resultó una preselección compuesta por 26 adolescentes aficionados a las matemáticas (de nuestro sistema educativo tamaulipeco). Enseguida se presentan los 4 problemas del examen (con sus soluciones) y, al final se añaden algunos comentarios sobre los problemas y los resultados del concurso.
Los problemas
1A. Factorizar la ecuación cuadrática $2011x^2+2012x+1=0$.
Solución
Es fácil darse cuenta que una de sus raíces es -1 (dado que la satisface). Y dividiendo entre $x+1$ se obtiene que la ecuación se factoriza como
Los problemas de la XXVII OIM (Cochabamba 2012)
Como se sabe, la Olimpiada Iberoamericana de Matemáticas se realizó esta semana en Cochabamba. Enseguida presento los problemas tomados del facebook de la OMM (de una comunicación de Amanda Rhoton).
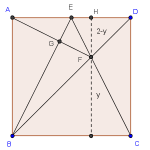
Equiláteros en un rectángulo
Inicia proceso de selección OMM Tamaulipas 2012
Tarde pero sin sueño --como dicen en Viento Libre--, el proceso de selección de la OMM en Tamaulipas inicia en este mes de septiembre. Así que se les notifica (de manera extraoficial) a todos los adolescentes interesados en las matemáticas de Tamaulipas para que se preparen para la etapa municipal. El calendario es el siguiente:
ORO para México --en la IMO 2012
Felicidades para la delegación mexicana. Y obviamente para Diego.
Los saluda
jmd

IMO 2012 (día 2)
4. Hallar todas las funciones $f:Z\rightarrow Z$ que cumplen la siguiente igualdad:
$$f(a)^2+f(b)^2+f(c)^2=2f(a)f(b)+2f(b)f(c)+2f(c)f(a).$$
para todos los enteros $a,b,c$ que satisfacen $a+b+c=0$
($Z$ denota el conjunto de los números enteros.)
5. Sea $ABC$ un triángulo tal que $\angle{BCA}=90$, y sea $D$ el pie de la altura desde $C$. Sea $X$ un punto interior del segmento $CD$. Sea $K$ el punto del segmento $AX$ tal que $BK=BC$. Análogamente, sea $L$ el punto del segmento $BX$ tal que $AL=AC$. Sea $M$ el punto de intersección de $AL$ y $BK$. Demostrar que $MK=ML$
6. Hallar todos los enteros positivos $n$ para los cuales existen enteros no negativos $a_1,a_2\ldots,a_n$ tales que
Los problemas de la IMO 2012 (primer día) --Mar del Plata, Arg.
1. Dado el triángulo $ABC$, el punto $J$ es el centro del excírculo opuesto al vértice $A$. Este excírculo es tangente al lado $BC$ en $M$, y a las rectas $AB$ y $AC$ en $K$ y $L$, respectivamente. Las rectas $LM$ y $BJ$ se intersecan en $F$, y las rectas $KM$ y $CJ$ se intersecan en $G$. Sea $S$ el punto de intersección de las rectas $AF$ y $BC$. Demostrar que $M$ es el punto medio de $ST$.
2. Si los reales positivos $a_2,a_3,\ldots, a_n$ satisfacen $a_2\cdot a_3 \cdots a_n=1$, demostrar que
$$(a_2+1)^2(a_3+1)^3\cdots(a_n+1)^n \gt n^n$$
3. El juego de la adivinanza del mentiroso es un juego para dos jugadores $A,B$. Las reglas del juego dependen de dos enteros positivos $k,n$, los cuales son conocidos para ambos jugadores.
Examenes de la Olimpiada Iberoamericana de Matemáticas por fin en MaTeTaM
Ya habíamos agregado todos los exámenes de las Olimpiada Mexicana de Matemáticas, ahora por fin tenemos todos los exámenes de la Olimpiada Iberoamericana de Matemáticas.

Calendario dodecaédrico con origami 2012
Tarde pero seguro, aquí está el calendario dodecaédrico 2012. Hubieramos querido agregarle fechas importantes y sacar versiones por países ya que también les interesaba el calendario en Colombia y Argentina. Pero ya no nos dio tiempo.
Para hacer el calendario sólo tienen que descargar, imprimir, doblar y armar. Aquí está el video con las intrucciones de armado que hicimos para la versión 2010.
Resultados de Tamaulipas en la XXV OMM --y soluciones
Bueno, me equivoqué en el pronóstico de dos platas y dos bronces. El resultado para Tamaulipas en el concurso nacional de la XXV Olimpiada Mexicana de Matemáticas fue:
- Plata para Bernardo;
- Bronce para Germán;
- Mención para Alejandra.
Y pues, la noticia (de consolación) es que volvemos a las platas, las cuales estuvieron ausentes en 2010. Y puedo añadir que Bernardo no decepcionó y que la sorpresa fue Alejandra.
