Problema de Excalibur Probleam Corner 309

Enviado por Luis Brandon el 23 de Enero de 2009 - 15:31.

En un triángulo acutángulo ABC donde AB < AC. Sea H el pie de la perpendicular de A sobre BC y M el punto medio de AH. Sea D el punto de tangencia del incirculo del triangulo ABC en BC. La linea DM intersecta por segunda vez al incirculo en N. Probar que los angulos BND y CND son iguales.

Solución

Por:

jesus

Fecha:

24 Ene 2009

Solución:

Solución con proyectividades:

Consideremos $P$ el punto diametralmente opuesto a D en el incírculo. Llamemos $D'$ y $Q$ a la intersección de $PN$ con $BC$ y $AD$ respectivamente. La figura quedaría más o menos así:

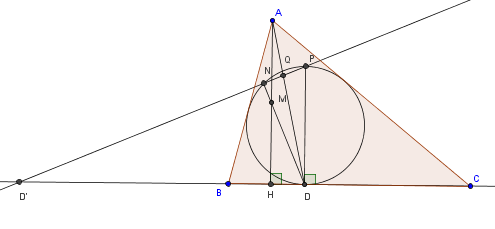
El conjugado armónico de $M$ con respecto al segmento $AH$ es el punto un punto al infinito $M'$ , pues $M$ es punto medio de $AH$ . Proyectando desde $D$ , sobre la recta $PN$ , al conjunto armónico $(AH, MM')$ se obtiene el conjunto $(QD', NP)$ . Es decir, se obtiene que $Q$ es el conjugado armónico de $D'$ con respecto a $NP$ .

Como obtuvimos que $Q$ es conjugado armónico de $D'$ con respecto a la cuerda $NP$ , se concluye que $Q$ está en la recta polar de $D'$ con respecto al incírculo. Y como, evidentemente, $D$ está la recta polar de $D'$ se tiene que $AD$ es la recta polar de $D'$ . Por el ejercicio El polo de la recta que pasa por el vértice y el punto de tangencia se observa que $D'$ es conjugado armónico de $D$ con respecto a $BC$ (pues es el punto polar de la recta $AD$ ).

Una vez probado que $D'$ es conjugado armónico de $D$ respecto a $BC$ y haciedo uso del ejercicio "Bisectriz, ángulo recto y conjugados armónicos" se puede ver que $ND$ es bisectriz del ángulo $BNC$ .

Que es lo que queríamos probar.

Solución sin proyectividades (la primera que se me ocurrió):

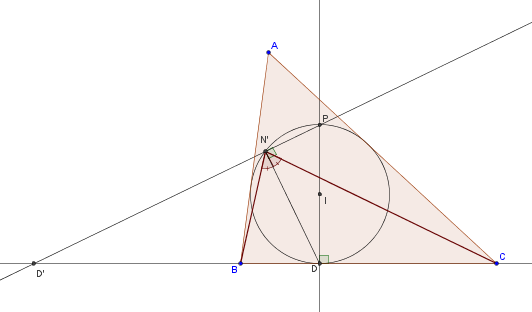
Consideremos D' el conjugado armónico de D con respecto al segmento AB. Luego, consideremos P el punto diagonalmente opuesto D con respecto a la circunferencia inscrita. Llamemos N' el otro punto de intersección de la recta PD' con el incírculo. Como DP es diámetro del incírculo y N' es un punto sobre la circunferencia, entonces, DN'P es un ángulo recto.

Ahora bien, por el ejercicio "Bisectriz, ángulo recto y conjugados armónicos" se puede ver que N'D es bisectriz del ángulo BN'C.

Nuestro objetivo ahora será demostrar que N' es igual a N, en consecuencia se tendrá resuelto el problema.

Para demostrar que N = N' bastará con demostrar que tan( $\angle N' DP$ ) = tan ( $\angle NDP$ ).

1. Cálculo de tan( $\angle N'DP$ ).

Observemos que tan( $\angle N' DP$ ) = tan ( $\angle PD' D$ ) = $2r / D'D$ .

Ahora bien, como D' es conjugado armónico de D, entonces se tiene que:

$\frac{D'C}{D'B}=\frac{DC}{BD}$

Llamemos $y = BD$ y $z = DC$ , entonce, se tiene la siguiente igualdad:

$\frac{z}{y}= \frac{D'C}{D'B}=\frac{D'B + BC}{D'B}= 1 + \frac{BC}{D'B} = 1 + \frac{BD + DC}{D'B}= 1 + \frac{y + z}{D'B}$

De aquí que:

$D'B = y\frac{z-y}{y+z}$

De esto último más el hecho de que $y= BD$ se obtenemos que:

$D'D = y\frac{z-y}{y+z} + y = \frac{2yz}{y+z}$

Por lo tanto:

$\tan ( \angle N' DC )= \frac{r(y+z)}{yz}= \frac{r}{y} + \frac{r}{z}$

Si llamamos $\alpha$ , $\beta$ y $\gamma$ a los ángulos en A, B y C del triángulo ABC. Podemos escribir la fórmula con tangentes:

$\tan ( \angle N' DC ) = \tan(\frac{\beta}{2}) + \tan(\frac{\gamma}{2})$

Con esta igualdad nos quedamos.

2. Cálculo de tan ( $\mathbold \angle NDP$ ).

Consideremos pues, N el punto del problema. Vamos a calcular $\tan{\angle NDP}$ .

Pero $\angle NDP = \angle DMH$ , entonces:

$\tan(\angle NDP) = \tan{\angle DMH } = \frac{HD}{HM} = \frac{BD - BH}{HM} = \frac{y}{HM} - \frac{BH}{HM}$

Luego, denotemos con $h = AH$ . Entonces, tenemos la siguiente igualdad:

$\tan{\angle NDP }= 2\frac{y}{h} - 2\frac{BH}{h}$

Es decir:

$\tan{\angle NDP } = 2\frac{y}{h} - \frac{2}{\tan(\beta)}$

Bueno, como sabemos,

$\tan(\beta) = \frac{2\tan(\frac{\beta}{2})}{1-\tan^2(\frac{\beta}{2})}$

Sustituyendo en expresión del ángulo obtenemos:

$\tan{\angle NDP } = 2\frac{y}{h} - \frac{1-\tan^2(\frac{\beta}{2})}{\tan(\frac{\beta}{2})}$

Es decir:

$\tan{\angle NDP } = 2\frac{y}{h} -\frac{1}{\tan(\frac{\beta}{2})} + \tan(\frac{\beta}{2})$

Ahora pasemos a unir las dos igualdades que hemos creado.

3. Demostremos que tan( $\angle N'DP$ ) = tan ( $\angle NDP$ ).

Bueno, la igualdad se da si y sólo si:

$\tan(\frac{\beta}{2}) + \tan(\frac{\gamma}{2}) = 2\frac{y}{h} -\frac{1}{\tan(\frac{\beta}{2})} + \tan(\frac{\beta}{2})$

Esto, si y sólo si:

$\tan(\frac{\gamma}{2}) = 2\frac{y}{h} -\frac{1}{\tan(\frac{\beta}{2})}$

Observemos que $y = \frac{r}{\tan(\frac{\beta}{2})}$ , y sustituyendo en la ecuación de arriba y haciendo unos despejes obtenemos:

$\frac{2r}{h} = 1 - \tan(\frac{\gamma}{2})\tan(\frac{\beta }{2}) \dots (1)$

Ahora bien, para demostrar esta igualdad usemos algunos hechos obvios. Primero definamos $x$ como la longitud de la tangente desde A al incírculo. Notemos que ya hemos definido $y$ y $z$ como las tangentes desde B y C respectivamente.

Entonces calculando el área del triángulo con base por altura y con lo del semiperímetro por el radio obtenemos la siguiente igualdad:

$\frac{h(y+z)}{2} = r(x+y+z)$

Es decir:

$\frac{2y}{h} = 1- \frac{x}{z+y+z}$

Entonces, para demostrar la igualdad (1) bastará con demostrar que:

$\frac{x}{z+y+z} = \tan(\frac{\gamma}{2})\tan(\frac{\beta }{2})$

Esta última igualad es fácil de demostrar gracias a las dos siguientes igualdad fáciles de probar:

$(x+y+z)\tan(\frac{\beta }{2}) = r_b$

$r_b\tan(\frac{\gamma}{2}) = x$

Donde $r_b$ es el radio de la circunferencia ex-inscrita opuesta al ángulo B.

Ver también:

Conjugados Armónicos (Definición)

Ver también:

El polo de la recta que pasa por el vértice y el punto de tangencia. (Problema)

Ver también:

Bisectriz, ángulo recto y conjugados armónicos (Problema)

Comentarios

#1 Guauuu tu solucion es

Enviado por Luis Brandon el 25 de Enero de 2009 - 21:52.

Guauuu tu solucion es demasiado creativa, esta, sin palabraste mandare la que yo tengo, es por ciclicos. para que la cheques, saludos, pd.no hay sugerencia para el de la cuerda,mediana y diametro?? hahah saludos chao.PDcuanto trabajo te costo ese problema???

La Geometria es el arte de pensar bien y dibujar mal...hahaha resolviendo con figuras falsas ahha brandoowin@hotmail.com

Inicia sesión o regístrate para enviar comentarios

#2 La verdad me costó toda la

Enviado por jesus el 26 de Enero de 2009 - 00:18.

La verdad me costó toda la tarde de antier resolverlo. Me pareció un problema muy bueno. Lo de usar los conjugados armónicos fué casi de inmediato, pero no sabía como usarlo. Busqué otras alternativas hasta que regresé a esta idea.

Desde que me dí cuenta que podía poner una igualdad usando sólo datos del triángulo supe que ya estaba el problema resuelto, pasó como una hora de manipulaciones algebraicas hasta que la reduje a la última igualdad. Se ve largo, pero en realidad son puras cuentas.

Ayer, antes de poner la solución, pensé en buscar otra usando el concepto de proyectividades, llegué a un par de cosas interesantes pero decidí mejor subir la solución de una vez. Si vuelvo a tener tiempo, haré una solución con proyectividades.

Espero que me mandes tu solución, apuesto a que es mucho más elegante.

Bueno, saludos Brandon y a ver si al rato pongo una sugerencia en el otro problema (cuerda, mediana y diámetro)

Jesús Rodríguez Viorato

Inicia sesión o regístrate para enviar comentarios

#3 Este problema esta propuesto

Enviado por Luis Brandon el 11 de Mayo de 2009 - 16:15.

Este problema esta propuesto en el mathematical exaclibur en el probleam corner Volumen 13, Numero 3, tarde pero seguro aqui va otra solucion espero y me entiendan, es la misma que le mande a Jesus.

Sea $I$ el centro del incirculo, $K$ el punto medio de $BC$ y sea $P$ la interseccion de $DM$ con la mediatriz de $BC$ , provare que el cuadrilatero $BPCN$ es ciclico y en consecuencia tendremos el resultado pedido, para ello es suficiente demostrar que $DN(DP)=DB(DC)$

Sean $a, b, c$ las medidas de los lados $BC, CA, AB$ respectivamente, y sea $s$ el semiperimetro del triangulo, de ahi es claro que $DB=s-b$ y que $DC=s-c$ . Sea $r$ el radio del incirculo y $(ABC)$ el area del triangulo. Sea $AH=h_a$ y $\angle{CDN}=\tau$

De ahi algunas equivalencias de $(ABC)$ son:

$ah_a/2=rs=\sqrt{s(s-a)(s-b(s-c)}$

Ahora las siguientes relaciones son claras(o mas bien faciles de provar)

$DK=DC-KC=\frac{a+b-c}{2}-\frac{a}{2}=\frac{b-c}{2}$

$DH=DB-HB=\frac{a+c-b}{2}-c\cos(\angle{ABC})=\frac{a+c-b}{2}-\frac{a^2+c^2-b^2}{2a}=\frac{(b-c)(b+c-a)}{2a}$
$=\frac{(b-c)(s-a)}{a}$

La Geometria es el arte de pensar bien y dibujar mal...hahaha resolviendo con figuras falsas ahha brandoowin@hotmail.com

Inicia sesión o regístrate para enviar comentarios

#4 Ademas De ahi tenemos

Enviado por Luis Brandon el 11 de Mayo de 2009 - 16:24.

Ademas $DN=2r sen\tau , DP=DK/\cos{\tau}=(b-c)(2 \cos{\tau})$ De ahi tenemos que

$DN(DP)=r(b-c) \tan{\tau}=r(b-c)\frac{MH}{DH}=r(b-c)\frac{h_a/2}{(b-c)(s-a)/a}$
$=r\frac{ah_a/2}{(s-a)}=\frac{rsrs}{s(s-a)}=\frac{(ABC)^2}{s(s-a)}=\frac{a(s-a)(s-b)(s-c)}{s(s-a)}=(s-b)(s-c)=DB(DC)$

Por consiguiente se sigue que el cuadrilatero $BPCN$ es ciclico...pero por que se cumple lo pedido...es claro no? como podras ver Jesus no es muy vistosa como tu solucion usando conjugados armonicos, pero se llega a lo pedidousando cosas poquito mas basicas, aunque no paresca larga si lo es....de los calculos faciles de probar se usa ley de cosenos , factorisaciones no muy faciles y una vez ley de senos y trigonometris!!!se podra sin ella?

saludos!!!!!

La Geometria es el arte de pensar bien y dibujar mal...hahaha resolviendo con figuras falsas ahha brandoowin@hotmail.com

Inicia sesión o regístrate para enviar comentarios

#5 Gracias por el piropo, pero

Enviado por jesus el 13 de Mayo de 2009 - 13:01.

Gracias por el piropo, pero yo creo que mi solución no es tan vistosa. Tiene eso de los conjugados armónicos, pero no es más que otra forma de atacar el problema. Yo siento que tu solución y la mía son muy similares: tu por un lado planteaste probar que un cuadrilátero es cíclico y yo por otro lado probar que la tangente de dos ángulos es la misma. Ambos, para hacerlo, tuvimos que pasar por una compleja manipulación de expresiones.

En mi caso, puede espantar el concepto de conjugados armónicos, pero es un concepto casi tan complicado como el de cíclicos. La difernencia entre estos dos conceptos es que el de conjugados armónicos es menos conocido y tratado como tema avanzado.

Yo sigo creyendo que una solución más padre sería con el uso de geometría proyectiva, o más específicamente, con proyectividades.

Saludos

Jesús Rodríguez Viorato

Inicia sesión o regístrate para enviar comentarios

#6 Lo intentaré en esta semana,

Enviado por Zzq el 11 de Mayo de 2009 - 20:58.

Lo intentaré en esta semana, se ve muy interesante. En el Excalibur luego ponen problemas muy bonitos, pero hay unos bien locochones que, ¡híjoles!, espantan a veces, jajaja xD. Gracias por la figura :D, intentaré unas cosas locas a ver si sale (la trigonometría me hace ojitos por lo mientras, jajaja xD). Saludoz.

|zzq|

Inicia sesión o regístrate para enviar comentarios

Problema de Excalibur Probleam Corner 309

Solución con proyectividades: