Te explico lo de convexidad... el resto no creo que le entiendas

Primero observemos que todas las diagonales $A_iA_{i+4}$ se bisectan en un punto (el baricentro); llamemos $G$ a dicho punto.

Ahora bien, para demostrar la conclusión del problema, bastará con probar que existe $i$ tal que $$\frac{B_iA_i}{GB_i} \leq 1/2 .$$

Por otro lado, llamemos $h_i$ a la altura bajada desde $A_i$ sobre el segmento $A_{i-1}A_{i+1}$ y llamemos $H_i$ a la altura bajada desde $G$ sobre $A_{i-1}A_{i+1}$. Con estos nuevos elementos, rescribirmos la conclusión en la forma equivalente: $$\frac{h_i}{H_i} \leq \frac{1}{2}.$$

Llamemos $\alpha_i$ el ángulo interno del octágono en el vértice $A_i$ y denotemos como $a$ la medida de los lados del octágono. De todos los $i$ elegimos el que tiene $\alpha_i$ lo más grande posible. Como consecuencia $\alpha_i \geq 135°$ (Ya que los ángulos internos del octágono suman 1080°).

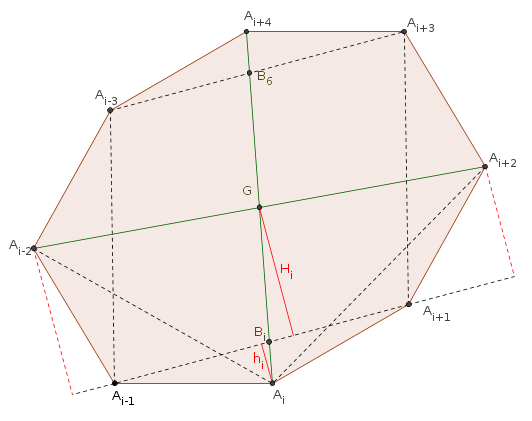
De la definición de $h_i$ se observa que $h_i = a \cos(\alpha_i)$.

Por otro lado, observemos que $H_i $ es el promedio de las alturas bajadas desde $A_{i+2}$ y $A_{i-2}$ sobre el segmento $A_{i-1}A_{i+1}$. Entonces, bastará demostrar que ambas alturas son mayores o iguales que $2h_i$ para lograr la conclusión de que $H_i \geq 2h_i$. Dichas alturas se calculan con la forma $a\sin(\alpha_{i \pm1} + \alpha_i/2 -90°)$. Entonces, bastará demostrar que $\sin(\alpha_{i \pm1} + \alpha_i/2 -90°) \geq 2\cos(\alpha_i/2)$.

Observemos primero que $(\alpha_{i -1} + \alpha_i/2 -90°) + (\alpha_{i +1} + \alpha_i/2 -90°) = 360° - \alpha_{i+2} > 180°$. Así que al menos uno de los sumandos es mayor o igual a 90°. Sin perdida de generalidad, podemos suponer que es $\alpha_{i +1} + \alpha_i/2 -90°  \geq 90°$.  Por otro lado, se tiene que $180° > \alpha_i \geq \alpha_{i+1}$; junto con la anterior desigualdad obtenemos que: $$180° > \frac{3}{2}\alpha_i - 90° \geq \alpha_{i +1} + \alpha_i/2 -90°  \geq 90° .$$

Como $\sin$ es decreciene entre 90° y 180°, entonces tedremos que:

\begin{eqnarray}
\sin(\alpha_{i+1} + \alpha_i/2 -90°) & \geq & \sin(3\alpha_i/2 -90°) \\
&= & -\cos(3 \alpha_i/2) \\
& = &\sin(\alpha_i)\sin(\alpha_i/2) - \cos(\alpha_i)\cos(\alpha_i/2)\\
& = & 2\sin^2(\alpha_i/2)\cos(\alpha_i/2) - \cos(\alpha_i)\cos(\alpha_i/2)\\
& = & \cos(\alpha_i/2)[2\sin^2(\alpha_i/2) - \cos(\alpha_i)]\\
& = & \cos(\alpha_i/2)[1 -2\cos(\alpha_i)]\\
&\geq& \cos(\alpha_i/2)\left[1 - 2\frac{-\sqrt{2}}{2}\right]\\
&=& (1+\sqrt{2})\cos(\alpha_i/2) \\
& > & 2\cos(\alpha_i/2)
 \end{eqnarray}

Si $\alpha_{i-1} + \alpha_i/2 -90° $ fuera mayor a $90°$ se podría concluir de igual forma que $\sin(\alpha_{i-1} + \alpha_i/2 -90°) \geq 2\cos(\alpha_i/2)$. Entonces la dificultad se da si suponemos que $\alpha_{i-1} + \alpha_i/2 -90° < 90°$. Pero en tal caso, tendremos que
\begin{eqnarray}
\alpha_{i-1} + \alpha_i/2 -90° &=& 450° -  \left(\frac{\alpha_i}{2} +\alpha_{i+1} + \alpha_{i+2}\right) \\
&=& (180° - \alpha_{i+2} ) + (270° - \alpha_i/2 - \alpha_{i+1})\\
&>& 270° - \alpha_i/2 - \alpha_{i+1}
\end{eqnarray}

Observemos además que $270° - \alpha_i/2 - \alpha_{i+1}$ es positivo. Como además $\sin$ es creciente de $[0, 90°]$, obtenemos que $\sin(\alpha_{i-1} + \alpha_i/2 -90°) > \sin(270° - \alpha_i/2 - \alpha_{i+1})$ y como ángulos complementarios tienen el mismo seno, tenemos que $\sin(270° - \alpha_i/2 - \alpha_{i+1}) = \sin(\alpha_{i+1} + \alpha_i/2 -90°)$ y este último satisface la desigualdad antes demostrada. Con lo que hemos concluido la prueba.

Nota, como logramos demostrar que $\sin(\alpha_{i+1} + \alpha_i/2 -90°) \geq (1+\sqrt{2})\cos(\alpha_i/2)$ entonces, la cota a demostrar se puede ajustar más. Es decir, hemos demostrado que existe $i$ tal que $$\frac{A_iA_{i+4}}{B_iB_{i+1}} \leq \frac{\sqrt{2} + 2}{\sqrt{2} + 1} = \sqrt{2},$$