Por dato, los triángulos $ ABC $ y $ BCD $ son semejantes. De aquí que $AB/BD=BC/DC=CA/BC.$ Es decir, nombrando de la manera usual a los lados de $ABC$, $c/BD=2a/b=b/a.$ Lo cual da lugar a las ecuaciones pitagóricas $2a^2=b^2$ y $c^2=2BD^2.$
Parecería que de estas ecuaciones nada se ha obtenido, pero por lo menos sugieren dos construcciones auxiliares --gracias a una evocación del teorema de Pitágoras. La ecuación $2a^2=b^2$ sugiere construir sobre el lado $b$ un isósceles rectángulo de lados $a$; y la ecuación $c^2=2BD^2$ sugiere construir sobre el lado $c$ un isósceles rectángulo de lados $BD.$
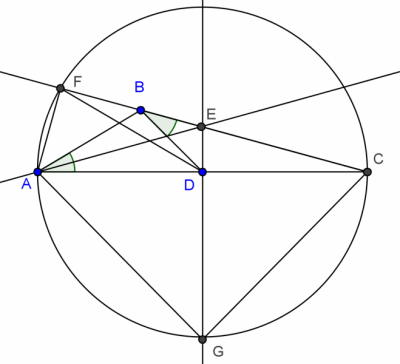
La primera construcción auxiliar sugerida por las ecuaciones se logra trazando el círculo de diámetro $AC (=b)$ con centro en el punto medio $ D.$ Y se ve que esta construcción también incluye a la otra que había quedado sugerida.
Porque, al prolongar $CB$ hasta cortar ese círculo en $F$ y trazar la mediana a la hipotenusa $AC$ del triángulo rectángulo $AFC$, se ve que $FBD$ es isósceles. Y esto porque la mediana a la hipotenusa define dos isósceles: $FCD$ es isósceles con ángulo en $ C $ de medida $x$, y $FDA$ es isósceles con ángulo en el vértice $D$ de medida $2x$ --central correspondiente al arco FA. Pero el ángulo $ADB$ es $3x$ --por ser externo en el triángulo $BDC$. Así que $FB=BD$ ($FBD$ es isósceles).
Aplicando Pitágoras al triángulo rectángulo $ABF$ se tiene $c^2=FB^2+FA^2$, es decir, $c^2=BD^2+FA^2.$ Pero ya sabíamos que $c^2=2BD^2.$ De aquí que $FA=FB=BD.$ Y se concluye que $ABF$ es isósceles rectángulo.
Focalizando de nuevo el triángulo isósceles $ADF$, debería ser claro --por los ángulos identificados hasta aquí-- que sus ángulos en la base son de $90-x$. Pero, en vista de que sabemos que $AFB$ es isósceles rectángulo, se tiene que $45=90-3x.$ Es decir, $x=15$ grados, y se logra ver que los ángulos $A,B,C$ del triángulo $ABC$ dado miden, respectivamente, $30,135, 15$ grados.

Es una de las soluciones que
Es una de las soluciones que di durante el examen, aunque me gusto mas la solucion que di de la construccion de un paralelogramo con ayuda de la mediatriz de AC, me parecio una solucion mas bonita.
Un buen problema seria asi(en la misma figura) Dado que D es punto medio de AC, y los angulos BAC y DBC iguales. Sabiendo que BDA mide 45...cuanto miden los angulos del triangulo ABC...
Tambien se nesesita almenos un trazo auxiliar, y no es tan facil diria que intermedio...saludos!!!!!
¿Cuál es tu solución con un
¿Cuál es tu solución con un paralelogramo? Me gustaría verla.
Ahi te va Jesus. Sean
Ahi te va Jesus.
Sean anguloBAC=2a=anguloDBC, y anguloACB=a
Prolonguemos BD hasta un punto E tal que ABCE sea un paralelogramo. Trazemos la mediatriz de AC(es claro que esta pasa por D) Sean P y Q los puntos en que la mediatriz corta a BC y AE, respectivamente. Es claro que los triangulos APC y AQC son isoseles con angulos en las bases iguales al anguloACB=a. De ahi es facil verificar anguloCQE=anguloCBE=2a. De ahi se tiene que el cuadrilatero BCEQ es ciclico y que anguloQBE=a, pero ademas anguloCAE=a entonces ABDQ es ciclicode ahi anguloBQD=anguloBAD=2a, y es claro que anguloBPA=2a, y que anguloAPD=90-a(este ultimo por el triangulo rectangulo APD) De ahi haciendo suma de angulos interiores al triangulo BPQ tenemos que...
180=angBQP+angQPB+angPBQ=6a+90 por lo que a=15...y de ahi se obtienen los angulos del triangulo...
Y perdon al no usar Latex
Y perdon al no usar Latex para las notaciones, lo que pasa es que le movieron la configuracion al teclado y ya no salen los mismos simbolos(estan en distinto orden,,,)y apenas los estoy aprendiendo...espero y de todas formas este clara!!!
Está super ingeniosa tu
Está super ingeniosa tu solución. La verdad me gustó. Es una construcción muy bonita. Te quedó muy padre.
Por otro lado, te comento que la mia fue con trigonometría y ley de senos. Sale muy rápido pero es árido.
Saludos y felicidades por tu muy buen resultados en el examen.
Muchas gracias jesus para que
Muchas gracias jesus para que tu digas que esta ingeniosa es por que realmente lo fue!!!
cabe mencionar que esa construccion la lleve a cabo ya que por la estructura del problema practicamente me lo gritava prolonga BD!!!!!! Por cierto me gustaria que vieras los dos ultimos problemas que puse y me digas que te parece, uno es mio y el otro es el de la revista de la olimpiada. En el segundo creo que si ves las sugerencias te daras cuenta de como lo hice saludos y gracias de nuevo!!!!