La figura que se deriva del enunciado sería más o menos como sigue (sin el arco $\widehat{BPA}$).
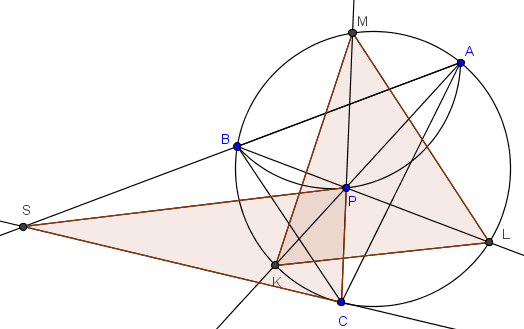
De acuerdo a los datos se tiene que $SC=SP$ y, por potencia de $S$, $SP^2=SC^2=SB\cdot SA$. Se sigue que $SP$ es tangente en $P$ al circuncírculo del triángulo $ABP$.
Queremos demostrar $\widehat{LM} =\widehat{MK}$.
Por el teorema de las cuerdas cruzadas se tiene
$$\angle KPC=\frac{\widehat{MA}+\widehat{CK}}{2}$$
Por tanto, $\widehat{MA}=2\angle{KPC}-\widehat{CK}$. De aquí que:
$$\widehat{LM}=\widehat{LA}+\widehat{AM}=\widehat{LA}+2 \angle{KPC}-\widehat{CK}$$
$$=2 \angle{SPK}+2 \angle{KPC}-\widehat{CK}$$
Porque $\widehat{LA}=2 \angle{SPK}$, dado que los arcos $PA$ y $LA$ son interceptados por el $\angle{PBA}=\angle{LBA}$, respectivamente.
$$=2 \angle{PCS}-\widehat{CK}$$
Por ser el triángulo $CPS$ isósceles.
$$=\widehat{MC}-\widehat{CK}$$
Pues el ángulo $MCS$ es semi-inscrito, con arco interceptado $MC$.
$$=\widehat{MK}+\widehat{CK}-\widehat{CK}=\widehat{MK}$$
Como se quería.

Mi solución: Sabemos que por
Mi solución:
Sabemos que $SC=SP$ por ser $SPC$ isósceles. Entonces $SC^2=SP^2=SB \cdot SA$ por potencia del punto $S$. De esta forma obtenemos que $SP$ es tangente al circuncírculo de $ABP$.
Definamos:
$\angle PAB=\alpha_1$
$\angle MCA=\theta_2$
$\angle CBL=\theta_1$
$\angle LBA=\beta_1$
$\angle KAC=\alpha_2$
Tenemos que $\angle SPB=\angle PAB=\alpha_1$ por ser el ángulo semi-inscrito al circuncírculo de $BPA$.
Sabemos que $\angle KPB=\alpha_1 + \beta_1$ por ser ángulo externo de $ABP$, entonces $\angle SPK=\beta_1$.
$\angle SCK=\alpha_2$ por ser semi-inscrito y abrir el arco $KC$.
$\angle KCB=\alpha_1$ por abrir el arco $KB$ al igual que $\angle KAB$.
Sabemos que $\angle ACL=\angle ABL=\beta_1$ por abrir el arco $LA$, aparte, $\angle KPC=\alpha_2 + \theta_2$ por ser ángulo externo al triángulo $APC$.
Como $SPC$ es isósceles, tenemos que $\angle SPC=\angle SCP$
de ahí que $\beta_1 + \alpha_2 + \theta_2=\alpha_2 + \theta_1 + \alpha_1$
luego, $\beta_1 + \theta_2=\theta_1 + \alpha_1$
sabiendo que $\angle MCL=\beta_1 + \theta_2$ y que $\angle KCM=\theta_1 + \alpha_1$, podemos concluir que $\angle MCL=\angle KCM$ de ahí que los arcos $KM$ y $ML$ sean iguales.. por lo tanto también sus cuerdas... así, concluimos que:
$KM=ML$ ■
Saludos.