Problemas - Teoría de números
Incentivo paternal
El padre quiere que su hija sea campeona en matemáticas de concurso. Le dice:"Por cada problema que resuelvas te daré 70 pesos y por cada uno que no resuelvas me darás 50 pesos." Después de intentar los n problemas de la lista que su papá le dio, la niña ha ganado 550 pesos. ¿Cuáles son los posibles valores de n?
Múltiplos de 11
Encontrar todos los números de tres cifras múltiplos de 11 , y tales que la suma de sus dígitos es 10, y la diferencia entre el número y el que resulta al invertir sus dígitos es 297.
Números en espiral
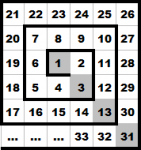
Considera la sucesión $\{1,3,13,31,\ldots\}$ que se obtiene al seguir en diagonal el siguiente arreglo de números en espiral.
Encuentra el número en la posición 100 de esa sucesión.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 2)
Para cada entero positivo $ n $ se define $a_n = n+m$, donde $ m $ es el mayor entero tal que $2^{2^m}\leq n2^n$. Determinar qué enteros positivos no aparecen en la sucesión $a_n$.
Olimpiada Iberoamericana (el 4 de 2008)
Demuestra que no existen enteros positivos $x,y$ tales que $x^{2008}+2008!=21^y$
Olimpiada Iberoamericana (el 4 de 2004)
Determinar todas las parejas $(a,b)$, donde $a,b$ son enteros positivos de dos dígitos cada uno, tales que $100a+b$ y $201a+b$ son cuadrados perfectos de cuatro dígitos.
Olimpiada Iberoamericana (el 5 de 1985)
A cada número natural n se le asigna un entero no negativo $f(n)$ de tal manera que se satisfacen las siguientes condiciones:
- (i) $f(rs)=f(r)+f(s)$
- (ii) $f(n)=0$, si el dígito de las unidades de n es 3
- (iii) $f(10)=0$
Hallar $f(1985)$
Olimpiada Iberoamericana (el 1 de 1999)
Halla todos los enteros positivos que son menores que 1000 y cumplen con la siguiente condición: el cubo de la suma de sus dígitos es igual al cuadrado de dicho entero.
Olimpiada Iberoamericana (el 4 de 1987)
Se define la sucesión $p_n$ de la siguiente manera: $p_1=2$ y, para $n\geq2$, $p_n$ es el mayor divisor primo de $p_1p_2\ldots p_{n-1}+1$. Demostrar que $p_n$ es diferente de 5.
Baldor debería saberlo...
El producto N de tres números enteros positivos es 6 veces la suma de tales números, y uno de los enteros es la suma de los otros dos. Calcular la suma de todos los valores posibles de N.
