División sintética --cálculo numérico de $P(x)/(x-c)$

En este post voy a presentar el conocido procedimiento de dividir un polinomio entre $x-c$ denominado división sintética.

División larga en polinomios

Consideremos la fracción racional $$\frac{x^3-2x^2-x+2}{x-1}$$ Y supongamos que deseamos efectuar la división con miras a simplificarla.El procedimiento algebraico de simplificación recurre a ciertos trucos de manipulación algebraica como sumar y restar la misma cantidad, factorizaciones parciales, etc. Veamos cómo opera ese método:
$$\frac{x^3-2x^2-x+2}{x-1}=\frac{x^2(x-1)-x^2-x+2}{x-1}=x^2+\frac{-x^2-x+2}{x-1}$$

Y tenemos ya un cociente parcial ($x^2$) más una fracción racional con numerador de un grado menor --lo cual nos permite volver a empezar, es decir, a repetir el mismo procedimiento con esa nueva fracción racional. El truco aquí fue una factorización parcial buscando cancelar.

Apliquemos de nuevo el procedimiento a
$$\frac{-x^2-x+2}{x-1}$$
Se tiene:
$$\frac{-x^2-x+2}{x-1}=\frac{-x^2-x+2x-2x+2}{x-1}$$

$$=\frac{-x(x-1)-2x+2}{x-1}=-x-\frac{-2x+2}{x-1}$$

Y, de nuevo, podemos volcer a empezar con la fracción $$\frac{-2x+2}{x-1}$$
La cual se simplifica a -2.
Reagrupando lo realizado se tiene que
$$\frac{x^3-2x^2-x+2}{x-1}=x^2-x-2$$
Trivial ¿no es cierto?

Pues no. Porque para el aprendiz ese procedimiento (que depende de trucos ad hoc) le resulta endiabladamente complicado. Y, pese a su complejidad, el adolescente aficionado a las matemáticas llega eventualmente a dominarlo.

Instancia de uso en el problem solving

Encontrar todos los enteros positivos $n$ tales que al dividir $7n + 4$ entre $2n – 1$ el resultado es un entero.

Solución

Primero hay que quitar del análisis la parte entera de $(7n + 4)/(2n - 1)$. Para ello observamos que $7n + 4 = 6n – 3 + n +7$. Al dividir entre $2n – 1$, lo que queda en duda entonces es si $n + 7$ entre $2n – 1$ es entero.

El resultado se puede obtener por tanteos. Los valores de $n$ que cumplen son: $1, 2, 3, 8$.

De manera alternativa $$\frac{7n+4}{2n-1}=\frac{6n – 3 + n +7}{2n-1}=3+\frac{n+7}{2n-1}$$ $$=3+\frac{1}{2}\frac{2n-1+15}{2n-1}=3+\frac{1}{2}(1+\frac{15}{2n-1})$$ Y el resultado se sigue buscando en los divisores de 15.

División de polinomios (método de la "casita")

Consideremos de nuevo la fracción racional
$$\frac{x^3-2x^2-x+2}{x-1}$$
Y supongamos que deseamos simplificarla.

Para ello se puede aplicar la división larga. El método se puede "leer" en las dos figuras siguientes:

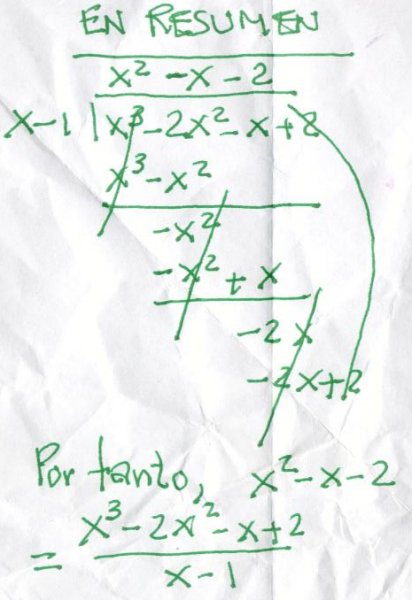
División sintética

Consideremos una vez más la fracción racional
$$\frac{x^3-2x^2-x+2}{x-1}$$
Una vez que uno se ha familiarizado con la división larga en polinomios, se puede observar que ciertos cálculos y cancelaciones son innecesarios.  Las siguientes figuras hablan por sí mismas (eso creo) --si el aprendiz hace un esfuerzo de comprensión...

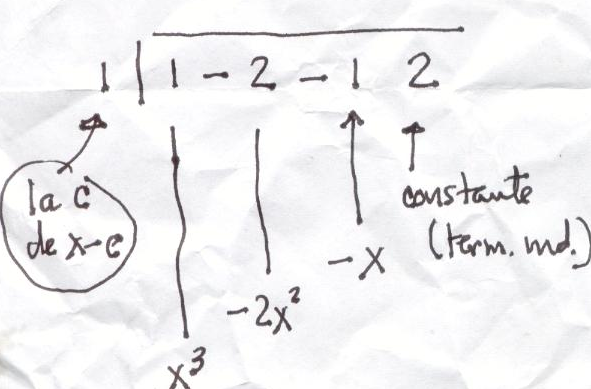
Como se puede ver en la figura anterior, el polinomio dividendo se expresa a través de sus coeficientes. La regla de lectura (y de escritura) es que el primer coeficiente es el de la $x$ al mayor exponente --digamos el de $x^n$--, el segundo exponente es el de $x^{n-1}$, etc. hasta llegar al último que es el término independiente. En cuanto al divisor, solamente se escribe la $c$ de $x-c$ ($x-1$ en este caso). La razón es casi obvia y se deja como ejercicio de reflexión para el lector.

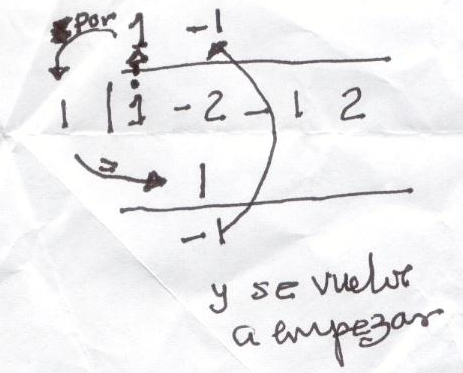
Una vez que se tiene la representación de la casita para la división, el siguiente paso es subir el primer coeficente, multiplicarlo por la $c$ del divisor $x-c$ y poner el resultado abajo del segundo coeficiente como muestra la figura.

Lo que sigue es sumar (esa es la razón por la que se pone $c$ y no $-c$ para representar el divisor $x-c$), y el procedimiento se vuelve a aplicar: subir, multiplicar, colocar el resultado abajo del siguiente coeficiente, sumar, etc. En la siguiente figura está el resultado.

Una vez teniendo el resultado de la división sintética lo que  sigue es decodificar. Pero eso es fácil pues sigue la misma regla que la escritura: el primer coeficiente del cociente (los números que quedan arriba de la casita) es el de la x con mayor exponente, etc.

Comentarios finales

Una de las razones que dificulta el aprendizaje de la división sintética es que la mayoría de los textos la presenta en un formato que no corresponde a la forma en que se efectúa la división de la "casita" en México.

La forma en que he presentado la división sintética hace eco de la división larga. Creo que eso ayuda a memorizar el procedimiento pues se apoya en uno ya conocido.

Pero, una vez que el aprendiz se ha familiarizado con la división sintética tal y como la he presentado aquí, puede hacerla "más sintética" aún observando que la colocación de los números arriba de la "casita" resulta redundante. Considere el siguiente ejemplo como ilustración de lo dicho.

Encontrar el cociente $Q(x)$ y el residuo $r$ al dividir $P(x)=x^3-3x^2+x+5$ entre $x-2$.

Solución eliminando redundancias (es el formato clásico; ver otros ejemplos en el sitio schollars.com.mx )

   2 | 1 -3   1  5
      |__ 2  -2 -2_
        1 -1  -1  3
Y hay que leer el resultado   1 -1 -1 3 como: el cociente es $x^2-x-1$ y el residuo es 3.

Lo cual es exactamente lo mismo que (la división sintética como la hemos presentado aquí):

        _1_-1_-1 _
    2 | 1  -3   1  5
       ____2_-2-2_
             -1  -1  3
Sólo que aquí el cociente se lee arriba de la casita (como en la división larga) y el residuo es el último número de abajo.

Insisto en que el aprendiz es muy sensible a los pequeños cambios y, según creo, es mejor usar al principo este último formato --pues es más cercano a la división larga y, por tanto, la codificación y la decodificación es más fácil de mantener en la memoria... el aprendiz decidirá cuándo está preparado para usar el formato clásico.

Los saluda

jmd

PD: Aquí les dejo este video de youtube que sí usa la casita en la división sintética.