Con cuadrados de lado 1 se forma en cada etapa una figura en forma de escalera siguiendo el patron del dibujo
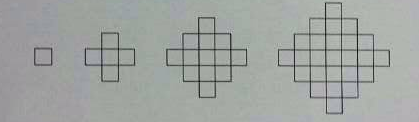
Por ejemplo, la primera etapa utiliza un cuadrado, la segunda utiliza 5. Determine la última etapa para la cual la figura correspondiente utiliza menos de 2014 cuadrados.

Primero, si no me equivoco,
Primero, si no me equivoco, este problema es el primer problema de la Olimpiada de Matemáticas de Centroamerica y el Caribe de este año.
Segundo, observemos que en realidad las figuras representan sumas de numeros impares consecutivos de la forma:
1+3+5+...+2n-1+...+5+3+1 , y su "regla" o "formula" es:
n^2 + (n-1)^2 . Como debe de ser menor que 2014, tenemos que
2(n^2-n) es menor que 2013, es decir, n^2-n es menor o igual a 1006,es decir, n(n-1) es menor o igual a 1006, por lo tanto n=32
Recordemos que n=32 por que
Recordemos que n=32 por que debe ser el mas proximo y menor a 2014
Yo me dí cuenta de que la
Yo me dí cuenta de que la diferencia entre el término 1 y 2 es 4, entre los términos 2 y 3 es 8 y entre 4 y 3 es 12 osea que las diferencias eran múltiplos de 4 consecutivas.
Hice la lista de los múltiplos de 4 y me dí cuenta de esto: 4,8,12,16, 20, 24,28,32,36,40, los números en negritas al sumarles 1 son los que usamos en la sucesión (llamémosle n) entre n1y n2 hay 1 múltiplo de 4, entre n2 y n3 hay 2 y entre n3 y n4 hay 3 lo que me llevó a la fórmula: 4[0+...+(n-1)]+1
Si sustituimos el valor de n nos damos cuenta de que si es la formula que soluciona la sucesión:
4[0+...+(1-1)]+1 = 4(0)+1= 1 4[0+...+(2-1)]+1 = 4(0+1)+1=5 4[0+... +(3-1)]+1 = 4(0+1+2)+1=13 4[0+...+(4-1)]+1 = 4(0+1+2+3)+1=25
A prueva y error sustituí el valor de n hasta llegar al número 32 que me dió como resultado 1984, cuando prové con 33 se pasó porque me dió 2113, así que la respuesta es 32.