Blogs
Una comunicación que calla: sobre el concepto de antiparalelas
Voy a ilustrar en este post la multiplicidad de conexiones que un cognizador debería establecer con una teoría previa en el momento de resolver (o estudiar la solución a) un problema de matemáticas escolares. Sostengo que la forma condensada de presentar las soluciones es una forma reticente de comunicar --así sea de manera involuntaria o por razones de estilo de redacción.
El cuadrado de Polya --con Geogebra
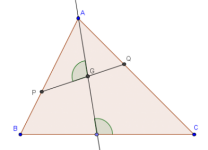
En este post comento sobre un posible proceso de solución al problema clásico de inscribir un cuadrado en un triángulo, usando el software de geometría dinamico Geogebra.
El cuadrado de Polya
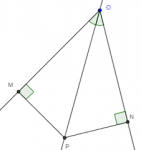
En el problem solving de las matemáticas escolares hay algunos problemas que son ya legendarios. Uno de ellos es el problema del cuadrado de Polya. Se trata de inscribir un cuadrado en un triángulo. A continuación su enunciado:
Inscribir un cuadrado en un triángulo $ABC$. Dos de los vértices del cuadrado deben estar en la base $BC$, y los otros dos en los otros dos lados, uno en cada uno.
Construcción de un triángulo... ¡con gestión del entusiasmo!
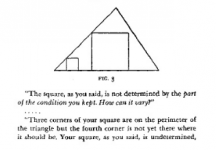
En este post voy a discutir la solución de un problema de construcción geométrica con regla y compás utilizando un enfoque al he llamado de entusiasmo --un poco para estar a la moda mass mediática de los libros de autoayuda y gestión del entusiasmo.
Para ilustrar el hecho de que el entusiasmo puede quedarse en el mero sueño si no es acompañado de una lógica sana, comparo mi método con los sueños de un desposeido en la canción americana "If I only had a match"
Dualidad en geometría
Ficciones matemáticas
El aspecto visual de las matemáticas y la conceptualización
Jean-Baptiste Lagrange --en español
Voy a presentar en este post a Jean-Baptiste Lagrange y su paper del año 2000 sobre la enseñanza de las matemáticas con tecnología (es decir, con software computacional).
Lo he traducido del francés y lo pongo a disposición de los usuarios de MaTeTaM, pues creo que desmitologiza las TICs y les da el lugar que les corresponde.
En lo que resta del post les presento a Jean-Baptiste Lagrange a través de su legendario ensayo del año 2000 denominado L'INTEGRATION D'INSTRUMENTS INFORMATIQUES DANS L'ENSEIGNEMENT: UNE APPROCHE PAR LES TECHNIQUES.
Conjeturar un lugar geométrico con Geogebra
Comunicación reticente --en los textos de matemáticas
Voy a comentar en este post la tesis de que, si el estudiante va a independizarse tarde o temprano de la escuela y continuar con su aprendizaje de manera autodidacta, lo mejor es que aprenda a leer libros. ("¿Quieres decir que los estudiantes no saben leer? No. Lo que quiero decir es que los libros siguen un cierto estilo de escritura con el cual hay que familiarizarse.") Ilustro la tesis con la redacción clásica de una solución a un problema. Y se empieza a aplicar un método de lectura que ha probado su eficacia en la práctica.
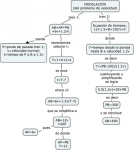
Dos problemas de velocidad
En este post comento dos problemas de velocidad ya en la sección de problemas de MaTeTaM. Le dedico más tiempo al más difícil, tratando de destacar la lógica de su solución. Al final presento un mapa conceptual del razonamiento y la simbolización del difícil, el cual parecería le da más estructura al proceso de resolución.