Avanzado
XXIV Olimpiada Iberoamericana de Matemáticas (problema 5)
La sucesión $a_n$ está definida por
$a_1=1, a_{2k}=1+a_k$ y $a_{2k+1}=\frac{1}{a_{2k}}$, para todo entero $k\geq 1$.
Demostrar que todo número racional positivo aparece exactamente una vez en esa sucesión.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 4)
Sea $ ABC $ un triángulo con $AB\neq AC$. Sean $ I $ el incentro de $ ABC $ y $ P $ el otro punto de intersección de la bisectriz exterior del ángulo $A $ con el circuncírculo de $ ABC $. La recta $PI$ intersecta por segunda vez al circuncírculo de $ ABC $ en el punto $J $. Demostrar que los circuncírculos de los triángulos $JIB$ y $JIC$ son tangentes a $IC$ y a $IB$, respectivamente.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 3)
Sean $C_1$ y $C_2$ dos circunferencias de centros $O_1$ y $O_2$, con el mismo radio, que se cortan en $A $ y en $ B $. Sea $P $ un punto sobre el arco $AB$ de $C_2$ que está dentro de $C_1$. La recta $AP$ corta a $C_1$ en $C $, la recta $CB$ corta a $C_2$ en $D $ y la bisectriz del $\angle CAD$ intersecta a $C_1$ en $E $ y a $C_2$ en $L $. Sea $F $ el punto simétrico a $D $ con respecto al punto medio de $PE$. Demostrar que existe un punto $X $ que satisface $\angle XFL = \angle XDC = 30^\circ$ y $CX = O_1O_2$.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 2)
Para cada entero positivo $ n $ se define $a_n = n+m$, donde $ m $ es el mayor entero tal que $2^{2^m}\leq n2^n$. Determinar qué enteros positivos no aparecen en la sucesión $a_n$.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 1)
Sea $ n $ un natural mayor que 2. Supongamos que $ n $ islas están ubicadas en un círculo y que entre cada dos islas vecinas hay dos puentes como en la figura:
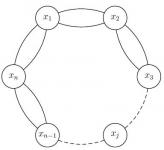
Olimpiada Iberoamericana (el 4 de 2004)
Determinar todas las parejas $(a,b)$, donde $a,b$ son enteros positivos de dos dígitos cada uno, tales que $100a+b$ y $201a+b$ son cuadrados perfectos de cuatro dígitos.
Olimpiada Iberoamericana (el 5 de 1985)
A cada número natural n se le asigna un entero no negativo $f(n)$ de tal manera que se satisfacen las siguientes condiciones:
- (i) $f(rs)=f(r)+f(s)$
- (ii) $f(n)=0$, si el dígito de las unidades de n es 3
- (iii) $f(10)=0$
Hallar $f(1985)$
Olimpiada Iberoamericana (el 4 de 1987)
Se define la sucesión $p_n$ de la siguiente manera: $p_1=2$ y, para $n\geq2$, $p_n$ es el mayor divisor primo de $p_1p_2\ldots p_{n-1}+1$. Demostrar que $p_n$ es diferente de 5.
Sin Euler estaríamos perdidos
Encontrar las tres últimas cifras de $2009^{9999}$ (argumento fiador requerido).
Divisible entre la suma de sus cifras
Demostrar que en un conjunto de 18 números enteros positivos, consecutivos y menores o iguales a 2009, hay uno que es divisible entre la suma de sus cifras.
