Publicaciones Recientes
Un problema de edades realmente difícil
Beto tiene el doble de la edad que Sara tenía cuando Beto era de la edad que ahora tiene Sara. Si la suma de las edades de Sara y Beto es 28 años, calcular sus edades.
Análisis de algunos problemas ENLACE 2012
Adán y su abuela --un singular problema de edades
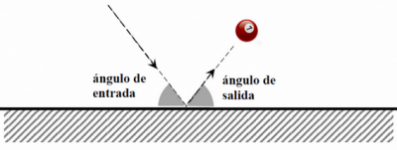
Billar culichi --en triángulo equilátero
En Culiacán tienen un juego de billar con mesas que tienen la forma de triángulo equilátero --cuyos lados miden 2 metros. El campeón de este juego es capaz de realizar un tiro de manera que la bola empieza en un vértice y, después de rebotar exactamente una vez en cada uno de los lados de la mesa, termina en otro vértice. Los rebotes en los lados de una mesa son tales que el ángulo de entrada es igual al ángulo de salida. Calcula la distancia que recorre la bola de billar al realizar ese trayecto.
Conjuntos cuadrilibres
Un subconjunto del conjunto {1,2,3,4,5,6,7,8,9,10} se dice cuadrilibre si la suma de los elementos de cualquier subconjunto de él no es un cuadrado. Por ejemplo, el subconjunto {1,3,8} no es cuadrilibre ya que tanto {1} como {1,8} son subconjuntos de él. ¿Cuál es el tamaño más grande que puede tener un subconjunto cudrilibre?
Números culichi
Un número de tres cifras abc se llama culichi si cumple al mismo tiempo las siguientes condiciones:
- al elevar al cuadrado el número abc se obtiene el número de cinco cifras defgh
- al elevar al cuadrado el número cba (que también es de tres cifras) se obtiene el número de cinco cifras hgfed.
Encuentra todos los números culichis.
Números lobola
Un número lobola es un número formado por 10 dígitos diferentes que cumple las siguientes características:
- abcdefghij son sus dígitos
- abcd es divisor de 2013
- cde y ef son múltiplos de 13
¿Cuántos números lobolas diferentes se pueden formar?
Números sinaloenses
Una pareja de enteros positivos $a$ y $b$ se llaman sinaloenses si $20a+13b=2013$ y $a+b$ es un múltiplo de 13. Encuentra todas las parejas sinaloenses.
¿Cacería de ángulos? Sí, pero con trazo auxiliar...
Sea $ABC$ un triángulo tal que sus ángulos $B$ y $C$ miden 100 y 62 grados, respectivamente. Sobre los lados $AB$ y $AC$ se toman los puntos $M$ y $N$, respectivamente, tales que $\angle{MCB}=52, \angle{NBC}=80$. Obtén la medida de $\angle{CMN}$
Problemas ONMAPS 2013 --secundaria
El concurso de la ONMAPS 2013 celebrado la semana pasada en Culiacán, Sinaloa, consideró (as usual) cuatro categorías: primaria, y los tres grados de secundaria. De esta manera, se aplicaron 4 exámenes de 6 problemas cada uno, uno por cada categoría y en dos días (tres problemas por día).