Blogs
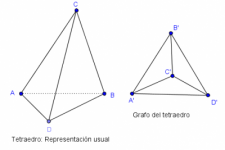
Grafos --y la modelación de relaciones
En este post la noción matemática de grafo es presentada a través de la metáfora de los poliedros y la relación de adyacencia entre sus vértices. Y ello para darle la vuelta a las definiciones formales, y ahorrarnos al menos cuatro definiciones: vértice, arista, la relación de adyacencia entre vértices, y la de incidencia entre vértices y aristas.
Crash Override --en la X Olimpiada Norestense de Matemáticas
En Hackers, el film ya clásico de 1995 (inicios de la era de Internet), Dade "Zero Cool" Murphy adopta su nuevo alias durante una operación de hackeo en donde es expulsado de la Red por otro hacker que se hace llamar "Acid Burn" (Kate Libby, interpretada por Angelina Jolie). El nuevo alias que adoptó Dade fue "Crash Override"
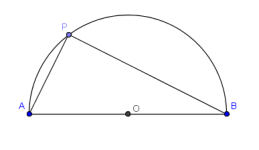
Solución errónea del último problema de la norestense.
En este post quiero presentar una solución del último problema de la norestense que casi me convence. Invito a los lectores de MaTeTaM a encontrar el error y comentarnos sus impresiones. Y claro, también, si tienen una solución al problema no duden en compartirla.

La dialéctica entre técnica y teoría
La dialéctica es un método de razonamiento que se basa en la contradicción: cada afirmación (tesis) tiene una antítesis que la contradice; y del enfrentamiento entre ambas surge una síntesis que elimina la contradicción (y la síntesis se convierte en la nueva tesis que encontrará su antítesis, etc.)
¿Es el aprendizaje del álgebra un problema resoluble con tecnología?
La computadora, se ha dicho, es una solución en busca de problemas. Y en la enseñanza de las matemáticas se postuló, desde la aparición de esa herramienta maravillosa, que la PC (y, antes de ella, las calculadoras) podría ser la solución a las dificultades que los estudiantes enfrentan al aprender esa "ciencia incomprensible" (la etiqueta es espuria, pero de aceptación universal) denominada álgebra .
Sobre el principio de no contradicción
El año pasado, al iniciar los entrenamientos de la preselección Tamaulipas para la Olimpiada Mexicana de Matemáticas, les presenté a los preseleccionados el "teorema" clásico de que todos los triángulos son isósceles (Ver mi post Lapsus de razonamiento para una "demostración" ).
Después de presentar la figura a mano alzada en el pizarrón (de hecho, la figura es la fuente de toda la confusión) Luis Brandon pasó al frente y realizó la "demostración" (pues ya la conocía y sabía que estaba trucada).
Lapsus de razonamiento en el problem solving
El lapsus (literalmente, resbalón o desliz), también llamado acto fallido o parapraxis, es un error cometido por descuido (según el DRAE).
Lapsus afectivos y lapsus cognitivos
El tema lo aborda Freud en su libro Psicopatología de la Vida Cotidiana, en donde atribuye el lapsus a una relajación del control consciente de lo reprimido --el lapsus sería el afloramiento de lo reprimido en los momentos en que los controles de la atención y/o la voluntad se debilitan.

Sobre la utilidad de las construcciones geométricas
De mis tiempos de escuelante recuerdo dos construcciones geométricas: el triángulo equilátero y el hexágono. Nada más fácil que tomar el compás, abrirlo a la medida del lado y hacer arcos que marcan los vértices. La justificación del por qué funcionan no era algo que se preguntara por el profesor ni era de nuestro interés adolescente.
El estudiante medianamente responsable hace las tareas de acuerdo al procedimiento, interpretado éste de manera literal, y se olvida (mejor dicho, se va con los amigos). Tampoco se preguntaba uno para qué servía eso.
Inferencias elementales a partir de la congruencia de ángulos
Este post, al igual que el anterior, se inscribe en la Reforma al Bachillerato (Bloque I, Matemáticas II). En él voy a elaborar (discutir) sobre los procesos de inferencia que pueden realizarse en configuraciones geométricas muy básicas, utilizando el concepto de ángulos congruentes. Y algunos resultados muy básicos, como el de la suma de los ángulos interiores de un triángulo, las relaciones de complementariedad y suplementariedad de dos ángulos.
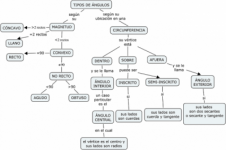
Clasificación de ángulos
Parecería que de ángulos hay muy poco que decir. Son los objetos geométricos que se miden con un transportador ¿cierto? Cierto, pero hay toda una terminología escolar que el aprendiz debería aprender.
En lo que sigue voy a hablar primero de una clasificación de los ángulos, y en la segunda parte voy plantear la clasificación de las relaciones entre dos ángulos. En cada una de esas clasificaciones se presenta primero un mapa conceptual y después se hace el mismo planteamiento pero de manera discursiva.