Blogs
Un ejercicio de prueba biyectiva en combinatoria
Como se sabe, el número de elementos del producto cartesiano de dos conjuntos finitos es el producto de las cardinalidades de los conjuntos. Pero aquí vamos a exhibir una demostración de ese hecho aplicando una prueba biyectiva de $|A \times B| = |A| |B|$.
Para demostrarlo vamos a definir una función entre el producto cartesiano $A\times B$ y el conjunto de enteros $S = \{0, 1, ..., |A||B| - 1\}$.
Arco capaz: un problema de lugar geométrico
En este post voy a definir el problema de lugar geométrico denominado arco capaz y a discutir el procedimiento de su construcción.
El problema y su procedimiento de construcción
En el problema de lugar geométrico denominado arco capaz, se da un segmento $AB$ y un ángulo $\lambda$. Se pide describir el lugar geométrico de los puntos en el plano, desde los que el segmento $AB$ se ve desde un ángulo $\lambda$.
Para quienes tienen prisa, el procedimiento de construcción es el siguiente:
Invariantes: un frame que permite razonar por el absurdo
Invariantes
(Adaptado de http://boumbo.toonywood.org/xavier/old/maths/stmalo/base-cours.pdf )
Se tiene un conjunto de configuraciones (por ejemplo, estados o posiciones en un juego). A una configuración inicial se le aplica una transformación (una jugada) sujeta a ciertas reglas (las reglas del juego) y sobre la configuración resultante se aplica otra transformación de acuerdo a las mismas reglas (el juego sigue). Se pide decidir si una cierta configuración puede o no obtenerse mediante transformaciones válidas partiendo de una configuración inicial.
Cuadrados perfectos
Cuadrados perfectos
Un cuadrado perfecto, en la terminología de la teoría de números, es un número que puede ser expresado como el cuadrado de otro. A continuación vamos a enunciar y a demostrar algunos teoremas acerca de los cuadrados perfectos.
Teoremas básicos
Teorema -1
Teorema. Si$ k $ es un cuadrado perfecto, los exponentes en su factorización prima son todos pares.
Álgebra como lenguaje (a propósito del problema de álgebra)
Sumas aritméticas
Las sumas aritméticas son importantes debido a su constante aparición en diferentes áreas de la ciencia. Un ejercicio elemental que servirá de motivación es el siguiente.
Se desea construir un pirámide con ladrillos como se muestra en la figura de abajo (con tres ladrillos en la punta y con varios escalones, un escalón superior tiene un ladrillo menos que el inmediato anterior). Pero con la diferencia de que en la base se quieren tener 100 ladrillos, ¿Cuántos ladrillos se necesitan?
Segmentos Dirigidos
Este concepto se oye mucho en las Olimpiadas de Matemáticas, pero --como muchos otros de olimpiada-- no es un tema que se enseñe en bachillerato. Esto puede llegar a asustar a muchos estudiantes, pero en realidad es un tema al que nada hay que temerle. Es muy fácil de entender y sobre todo es muy útil.
La idea principal de los segmento dirigidos es agregar una propiedad extra a la noción de segmento. Esta propiedad se resume así:
Estos eran dos amigos...
B: Ah…Mmhh… Creo que esa sí me la sé. Es base por altura. ¿Cierto?
A: ¿Pero si no te dan la altura?
B: Bueno, pues ¿qué te dan?
A: Te dan las longitudes de los lados.
B: Bueno, entonces saco la altura con el seno del ángulo ¿te dan un ángulo?
A: No.
B: Ah pues deja ver…Creo que se puede eliminar el seno utilizando la ley de cosenos… eso lo hice una vez cuando estudié la secundaria… Deja ver si me sale…
$2(ABC) = ah = absenC$ ¿OK?
A: Con $(ABC)$ estás denotando el área del triángulo $ABC$ ¿no es así?

Problema, semana 18-22 de Feb.
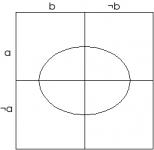
Diagrama de Lewis Carroll
Es una variante del diagrama de Venn-Euler que facilita la clasificación de un universo $S$de objetos según tres atributos $a$, $b$ y $c$. La clasificación es dicotómica: cada objeto de $S$ ya sea tiene la propiedad o atributo $a$, $b$, o $c$ o bien no la tiene (esto último se representa con ¬$a$, ¬$b$, o ¬$c$).