Blogs
Problemas del primer selectivo OMM_Tam_2011
En este post presento los 7 problemas del primer selectivo aplicado a la preselección Tamaulipas OMM 2011 y se añaden sugerencias para sus soluciones. Los problemas son elementales y no deberían presentar mayores dificultades para al menos la mitad de los preseleccionados.
Introducción
Atendiendo una invitación de Ramón Llanos, el primer entrenamiento de la preselección Tamaulipas de la Olimpiada Mexicana de Matemáticas, Delegación Tamaulipas, estuvo a mi cargo.
En ese entrenamiento pude concretizar la propuesta de entrenamiento hecha en el post anterior denominado El difícil del estatal
El difícil del estatal (OMM_Tam_2011)
Es glotón y cuenta doble: sobre el fácil del estatal
El problema 1 del concurso estatal (OMM Tamaulipas 2011) es más difícil de lo que parece (si se hubiese exigido la demostración). Es el siguiente (elegido de un lote de problemas que le enviaron al delegado desde el comité organizador nacional de la OMM):
En una reunión de 6 personas, éstas se saludaron de mano. Si se sabe que sólo una saludó a todos ¿cuál es el máximo número de apretones de mano que pudo haber en dicha reunión?
El contexto auténtico en problemas matemáticos: el caso (único) de PISA
En este post voy a discutir la posible relevancia de los problemas tipo PISA en la enseñanza de las matemáticas. Se presentan dos ejemplos: la dificultosa identificación de una gráfica (de modelación y difícil contenido matemático) y uno fácil de contexto auténtico, para cuya respuesta basta con analizar sin miedo los datos (extrayendo conclusiones) . Al final se proponen algunas lecciones que deja el examen PISA para los sistemas educativos.
Kafka en México --y la reforma 2011 en normales
En este post voy a comentar la reforma 2011 en normales, la cual aumenta a 5 años la duración de sus licenciaturas e incluye matemáticas como una de las materias a cursar. El evento es importante para la educación mexicana y atiende una recomendación de la OCDE del año pasado (mejorar la formación de sus profesores). Cito de mi post PISA, OCDE-recomendaciones y el efecto Casandra tal recomendación:
Prototipos, ejemplos generales y categorización
Voy a elaborar en este post sobre un tema que atrajo mi atención hace algunos meses y que en estos días volví a estudiar. Es el tema de los prototipos --y su utilidad en la educación matemática.
¿Definir o no definir?
Si bien es cierto que las matemáticas escolares o, mejor dicho, la didáctica de las matemáticas escolares, rehuyen las definiciones, también lo es que en los cursos universitarios de matemáticas, y ciertamente en las matemáticas de concurso, las definiciones formales son imposibles de evitar (bueno, si es que realmente se quiere enseñar y aprender matemáticas y entrenar y ganar concursos).
El Cuadrado de Sócrates --y los triángulos notables
Voy a discutir en este post cuatro problemas de geometría básica que se resuelven de manera elemental invocando dos triángulos notables. Estos triángulos son el isósceles rectángulo (la mitad de un cuadrado) y el 30-60-90 (la mitad de un triángulo equilátero). En los dos problemas de inicio, la solución presentada invoca el isósceles rectángulo; en los otros dos se debe invocar la mitad de un equilátero.
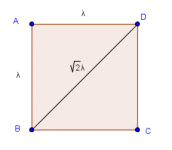
Primer problema (el Cuadrado de Sócrates)
Dado el lado $\lambda$ de un cuadrado, construir el cuadrado del doble de área.
Solución
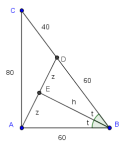
Sobre la utilidad de saber trigonometría
Método de áreas (2a parte)
En este post voy a discutir el método de áreas en el problem solving de matemáticas de concurso. El tema ya lo había discutido (un poco de manera reticente) en el post Método de áreas. En esta ocasión voy a profundizar un poco más en ese método, presentando y demostrando un teorema --y algunas de sus instancias de uso.
Discusión sobre incírculos y excírculos
Voy a discutir en este post algunos conceptos relacionados con las circunferencias incrita y exinscrita. Dichos conceptos forman un todo y conviene aprenderlos en paquete --es muchísimo más fácil retenerlos en la memoria y comprenderlos si se aprenden en sus interconexiones.
Se trata de los conceptos de semiperímetro --en el contexto de ciertas simetrías entre las longitudes de las tangentes de circuncírculo y excírculos--, el concepto de puntos isotómicos, y el de los puntos de Gergonne y Nagel --como ejemplo de puntos conjugados isotómicos.
