Problemas - Combinatoria
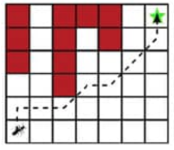
La hormiga, el mago y la lava (OMM 2021 P3)
Sean $m,n \geq 2$ dos enteros. En una cuadrícula de $m \times n$, una hormiga empieza en cuadrito inferior izquierdo y quiere camina al cuadradito superior derecho. Cada paso que da la hormiga debe ser a un cuadrito adyacente, de acuerdo a las siguientes posibilidades $\uparrow$, $\rightarrow$ y $\nearrow$. Sin embargo, un malvado mago ha dejado caer lava desde arriba y ha destruido algunos cuadritos de forma tal que:
Problema clásico con solución atípica
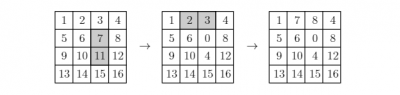
En una cuadrícula de $ n \times n$ se escriben los números del 1 al $n^2$ en orden, por renglones, de manera que en el primer renglón aparecen los números del 1 al n, en el segundo los números del n+1 al 2n, y así sucesivamente. Una operación permitida en la cuadrícula consiste en escoger cualesquiera dos cuadraditos que compartan un lado y sumar (o restar) el mismo número entero a los dos números que aparecen esos dos cuadraditos. Por ejemplo, aquí abajo se muestran dos operaciones sucesivas permitidas en una cuadrícula de 4x4: primero restando 7 a los cuadraditos sombreados y luego sumando 5 a los sombreados.
Problema 2. 29a Olimpiada Mexicana de Matemáticas
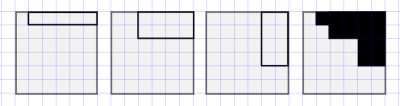
Sean $n$ un entero positivo y $k$ un entero entre $1$ y $n$. Se tiene un tablero de $n \times n$ color blanco. Se hace el siguiente proceso. Se dibujan $k$ rectángulos con lados de longitud entera, con lados paralelos a los del tablero y tales que su esquina superior derecha coincide con la del tablero. Luego, estos $k$ rectángulos se rellenan de negro. Esto deja una figura blanca en el tablero. ¿Cuántas figuras blancas diferentes podemos obtener, que no se puedan obtener haciendo el proceso con menos de $k$ rectángulos?
Focos distribuidos en una circunferencia (P1)
Se tienen 25 focos distribuidos de la siguiente manera: los primeros 24 se disponen en una circunferencia colocando un foco en cada uno de los vértices de un 24-ágono regular, y el foco restante se coloca en el centro de dicha circunferencia. Se permite aplicar cualquiera de las siguientes dos operaciones:
Un cubo y muchos cubitos
Un cubo de $n \times n \times n$ está construido con cubitos de $1\times 1 \times 1 $, algunos negros y otros blancos, de manera que en cada uno de los subprismas de $n \times 1 \times 1 $, de $1 \times n \times1 $ y de $1 \times 1 \times n$ hay exactamente dos cubitos negros y entre ellos hay un número par (posiblemente 0) de cubitos blancos intermedios. Por ejemplo, en la siguiente ilustración, se muestra una posible rebanada de cubo de $6 \times 6 \times 6 $ (formada por 6 subprismas de $1\times{6}\times{1}$

Cambios de estado de focos en un tablero (P2)
En cada casilla de un tablero $ n\times n $hay un foco. Inicialmente todos los focos están apagados. En un paso, se permite cambiar el estado de todos los focos en una fila o de todos los focos en una columna (los focos prendidos se apagan y los focos apagados se prenden). Muestra que si después de cierta cantidad de pasos hay uno o más focos prendidos entonces en ese momento hay al menos n focos prendidos.
Cambios de estado en cuadrícula 6X6 --con luciérnagas
En cada cuadrado de una cuadrícula de $6\times6$ hay una luciérnaga apagada o encendida. Una movida es escoger tres cuadrados consecutivos, ya sean los tres verticales o los tres horizontales, y cambiar de estado a las tres luciérnagas que se encuentran en dichos cuadrados. (Cambiar de estado a una luciérnaga significa que si está apagada se enciende y si está encendida se apaga.) Muestra que si inicialmente hay una luciérnaga encendida y las demás apagadas, entonces no es posible hacer una serie de movidas tales que al final todas las luciérnagas estén apagadas.
Caballos en el tablero
Considera un tablero de ajedrez. Los números del 1 al 64 se escriben en las casillas del tablero como en la figura:
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
P5 OMM 2005. Con cualquiera de las restantes se completa
Sea $N$ un entero mayor que 1. En cierta baraja de $N^3$ cartas, cada carta está pintada de uno de $N$ colores distintos, tiene dibujada una de $N$ posibles figuras y tiene escrito un número entero del 1 al $N$ (no hay dos cartas idénticas). Una colección de cartas de la baraja se llama completa si tiene cartas de todos los colores, o si entre sus cartas aparecen todas la figuras o todos los números. ¿Cuántas colecciones no completas tienen la propiedad de que, al añadir cualquier otra carta de la baraja, ya se vuelven completas?
P6 OMM 2004. Cambios de dirección en cuadrícula 2004X2004
¿Cuál es el mayor número posible de cambios de dirección en un recorrido sobre las líneas de una cuadrícula de $2004\times 2004$ casillas, si el recorrido no pasa dos veces por el mismo lugar?
