Problemas - Geometría
Configuración con acutángulo isósceles
2.5. Sea ABC un triángulo acutángulo isósceles con AC=BC. M y N son los puntos medios de AC y BC, respectivamente. La altura desde A corta a la prolongación de MN en X y la altura desde B corta a la prolongación de MN en Y. Z es la intersección de AY con BX. Además, sucede que los triángulos ABC y XYZ son semejantes. Determina la razón $\frac{AC}{AB}$.
Ángulo postgiro
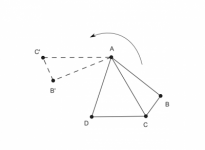
2.2. Sea ABCD un cuadrilátero que cumple: AB=AD,AC=BC+CD y los ángulos ABC y CDA suman 180 grados. El triángulo ABC se gira con centro en A formando el triángulo AB'C', como se muestra en la figura, hasta que el punto B' coincida con D, formándose el triángulo ADC'. Encuentra la medida del ángulo ACC'.
Isósceles inscrito en acutángulo
1.6. Sean ABC un triángulo acutángulo, H su ortocentro y M el punto medio de BC. La perpendicular a MH por H corta a AB en L y a AC en N. Demuestra que LH=HN.
Razón de áreas en un hexágono
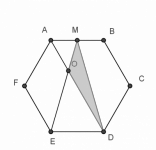
1.3. Sean ABCDEF un hexágono regular y M el punto medio del lado AB. Si O es el punto donde se cruzan los segmentos AD y ME ¿qué parte del área del hexágono es el área del triángulo OMD?
Ejercicio con rectángulo y punto medio
En un rectángulo ABCD, M es el punto medio de BC. Si T es el pie de la perpendicular a AM bajada desde D demostrar que CT=CD.
Ejercicio con diámetro y cuerda perpendicular
En un círculo de centro O, sean AB un diámetro, KM una cuerda perpendicular al diámetro AB y C el punto de intersección de la cuerda KM y el diámetro AB. ¿Cuál triángulo tiene mayor área, el BOK o el AOM?
Diagonales y triángulos de un cuadrado
En un cuadrado ABCD, las diagonales AC y BD se cruzan en E. Si la diagonal AC mide 12 ¿cuál es el área del triángulo BCE?
Bisectriz en la mitad de un cuadrado
Las diagonales de un cuadrado ABCD se cortan en E, la bisectriz del ángulo DBC corta a la diagonal AC en P y al lado CD en Q. Demostrar que DQ mide el doble que PE.
ONMAPS Tamaulipas 2014 - Problema 10
En el interior de un triángulo ABC se elige el punto P de tal manera que los ángulos PAC y PBC son iguales. Las perpendiculares desde P a BC y CA cortan estos lados en L y M, respectivamente. Si D es el punto medio de AB, demostrar que DL=DM.
Ostomachion, el cuadrado y sus partes
En el cuadrado ABGD, sea E el punto medio de BG por el que levantamos la perpendicular EZ a BG (Z en AD). Trazaos las diagonales AG (del cuadrado) y BZ y ZG (de los rectángulos definidos por EZ en cuadrado). AG y BZ se cortan en F. Por el punto medio H de BE levantamos la perpendicular HT (T en BZ). Por H trazamos el segmento HK (K en BZ) de tal manera que H,K y A estén alineados. Trazamoe el segmento BM con M punto medio de AL. Con esto hemos dividido el rectángulo ABEZ en siete partes.
