XIV ONMAPS 2014
Primaria resolvió los problemas 1,2,3.
Primer grado los problemas 2,3,4.
Segundo grado los problemas 3,4,5.
Tercer grado los problemas 4,5,6.
Coeficientes y raíces en tres cuadráticas
2.6. Considere las ecuaciones cuadráticas
\begin{eqnarray}
x^2-b_1x+c_1&=&0\\
x^2-b_2x+c_2&=&0\\
x^2-b_3x+c_3&=&0
\end{eqnarray}
con $b_1.b_2,b_3,c_1,c_2,c_3$ números reales diferentes.
¿Es posible que los números $b_1,b_2,b_3,c_1,c_2,c_3$ sean las raíces de las ecuaciones cuadráticas en algún orden?
Configuración con acutángulo isósceles
2.5. Sea ABC un triángulo acutángulo isósceles con AC=BC. M y N son los puntos medios de AC y BC, respectivamente. La altura desde A corta a la prolongación de MN en X y la altura desde B corta a la prolongación de MN en Y. Z es la intersección de AY con BX. Además, sucede que los triángulos ABC y XYZ son semejantes. Determina la razón $\frac{AC}{AB}$.
Tabla con números sin 3 o 7
2.4. Se tiene una tabla con siete columnas A,B,C,D,E,F,G y se coloca en ella los números naturales que no contienen al 3 o al 7 en su desarrollo decimal. Se empieza en la casilla C1, como se muestra. ¿En cuál columna y renglón queda el 2014?

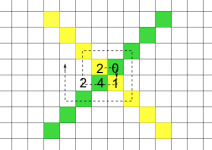
Espiral con el 2014 en cuadrícula
2.3. Sobre una cuadrícula se coloca 2014 veces el número 2014 (un dígito en cada casilla) siguiendo una espiral como se muestra en la figura. Sea M la suma de los números sobre las casillas verdes y N la suma de los números sobre las casillas amarillas. Calcula la diferencia entre M y N.
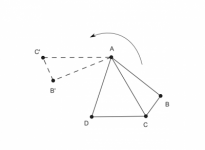
Ángulo postgiro
2.2. Sea ABCD un cuadrilátero que cumple: AB=AD,AC=BC+CD y los ángulos ABC y CDA suman 180 grados. El triángulo ABC se gira con centro en A formando el triángulo AB'C', como se muestra en la figura, hasta que el punto B' coincida con D, formándose el triángulo ADC'. Encuentra la medida del ángulo ACC'.
Huevos y chilaquiles en buffet
2.1. Cierto día en el restaurante La Cascada prepararon para el buffet de desayuno una charola de cada uno de los siguientes siete platillos: huevos con tocino, frijoles con queso, huevos con jamón, huevos a la mexicana, chilaquiles rojos, chilaquiles con huevo y chilaquiles verdes. Se le ordena al mesero acomodar las charolas de los platillos, alineadas en la barra, de forma tal que las que contengan huevo queden juntas y que las que contengan chilaquiles queden juntas.
Isósceles inscrito en acutángulo
1.6. Sean ABC un triángulo acutángulo, H su ortocentro y M el punto medio de BC. La perpendicular a MH por H corta a AB en L y a AC en N. Demuestra que LH=HN.
Ordenar los superhéroes
1.5. Heberto tiene en su colección de figuras de acción de superhéroes dos Hulk, dos Superman,dos Ironman, dos Batman que quiere acomodar en línea sobre una repisa. Quiere que entre cada dos superhéroes iguales haya una cantidad diferente de figuras. Por ejemplo, si hay tres figuras entre los dos Hulk, no podría haber tres figuras entre los dos Batman. De cuántas maneras diferentes puede hacer esto?
La lista de Julio
1.4. Julio hace una lista con los números que cumplen las siguientes condiciones:
--El número es de ocho cifras, todas diferentes.
--Es múltiplo de 8.
--Cada dos cifras adyacentes en el número forman un nuevo número que es múltiplo de 7 o de 13, aunque no necesariamente todos múltiplos del mismo número.
Encuentra los números de la lista de Julio.
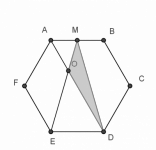
Razón de áreas en un hexágono
1.3. Sean ABCDEF un hexágono regular y M el punto medio del lado AB. Si O es el punto donde se cruzan los segmentos AD y ME ¿qué parte del área del hexágono es el área del triángulo OMD?