Problemas - Geometría
El 3 de Regiones
Sea $ ABC $ un triángulo rectángulo en $A$. La circunferencia con diámetro $AB$ corta a $ BC $ en $D$, y la circunferencia que pasa por $A, D,$ y el punto medio $O$ de $AB,$ corta a $CA$ en $P$ y corta nuevamente a $ BC $ en $Q$. Demuestra que $PQOA$ es un rectángulo.
Problema 1, geometrense 2008
En un circunferencia hay $3n$ puntos que la dividen en $3n$ arcos. De estos arcos $ n$ miden 1, $n $ miden 2 y el resto mide 3. Demuestra que existen dos de estos puntos diametralmente opuestos.
Ángulos en el reloj
¿Cuál es el ángulo que forman las manecillas del reloj a las 9:30? (Argumento fiador requerido.)
Problema 6, XII Olimpiada Iberoamericana
Sea $P=\{P_1, P_2, \dots, P_{1997}\}$ un conjunto de 1997 puntos en el interior de un círculo de radio 1, siendo $P_1$ el centro del círculo. Para cada $k=1, \dots, 1997$ sea $x_k$ la distancia de $P_k$ al punto de $ P$ más próximo a $P_k$ y distinto de $P_k$. Demostrar que:
$$x_1^2 + x_2^2 + \cdots +x_{1997}^2 \leq 9$$
P3. OMM 1993
Dentro de un pentágono de área 1993 se encuentran 995 puntos. Considere estos puntos junto con los vértices del pentágono.
Muestre que, de todos los triángulos que se pueden formar con los 1000 puntos anteriores como vértices, hay al menos uno de área menor o igual que 1.
El polo de la recta que pasa por el vértice y el punto de tangencia.
Sea $ ABC$ un triángulo y sean $ D$, $ E$ y $ F$ los puntos donde la circunferencia circunscrita es tangente al lado $ BC$, $CA$ y $ AB$. Llamemos $D'$ el punto donde la recta $EF$ corta a la recta $AB$. Demuestra que:
a) $D'$ es el conjugado armónico de $D$ con respecto al segmento $ AB$.
b) Que la recta $AD$ es la polar de $D'$ respecto al incírculo.
Demostrar cuadrado
Sea ABCD un cuadrilatero tal que los angulos internos en los vertices A, B, y C son de cuarenta y cinco grados. Demostrar que los puntos medios de los lados del cuadrilatero determinan un cuadrado.
Propuesto por: Fernando
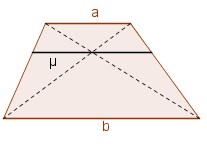
Media armónica de las bases de un trapecio.
Considere $\mu$ un segmento paralelo a las bases $a$ y $b$ de un trapecio, de tal manera que $\mu$ pasa por el punto de intersección de las diagonales y sus extremos están sobre los lados del trapecio. Demostrar que $\mu$ es la media armónica de $a$ y $b$, es decir:
Tres círculos congruentes
Tres círculos $C_1, C_2, C_3$ del mismo radio se intersectan no tangencialmente en un punto $P$. Sean $A, B$ los centros de $C_1, C_2$, respectivamente; y $C, D$ los puntos de intersección de $C_1, C_2$, respectivamente, con $C_3$. ($C, D$ son ambos diferentes de $P$.) Demostrar que $ABCD$ es un paralelogramo.
Cíclico en tres circunferencias tangentes
Considere $\mathcal{C}_1$, $\mathcal{C}_2$ y $\mathcal{C}_3$ tres circunferencia que por pares son tangentes externas. Llamemos $P$ y $Q$ los puntos de tangencia de $\mathcal{C}_1$ con $\mathcal{C}_2$ y $\mathcal{C}_3$ respectivamente.
