Problemas - Geometría
Equilátero inscrito en equilátero
Inscribir un triángulo equilátero en un triángulo equilátero $ ABC $, de tal manera que cada lado del inscrito sea perpendicular a un lado del triángulo $ ABC $. (Describir el procedimiento de construcción.)
Problema 6G, Ciudades 2009
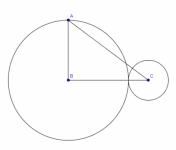
En la figura el segmento $ BC $ une los centros de los círculos tangentes, $AB$ es perpendicular a $BC, BC =8$ , y $AC =10$. Calcular el área de cada círculo.
¿Incírculo o excírculo?
Sean $D$ en $AB$ y $E$ en $AC$, los extremos de un segmento tangente al incírculo del triángulo $ ABC $. Si los lados $AB, BC, CA$ miden, respectivamente, $c, a, b$, expresar el perímetro del triángulo ADE en términos de $a, b, c$.
Medio rombo y un 30-60-90
Un rombo de lado $2m$ tiene un ángulo de $30^\circ$. ¿Cuánto vale su área?
Inradio y cateto
Expresar el radio $ r $ del incírculo de un triángulo rectángulo isósceles en términos del cateto $ c $.

Área de un equilátero
Sea ABC un triangulo equilátero y R el radio de la circunferencia que lo circunscribe, demuestre que el area del triangulo es igual a: $$ 3R^2\sqrt{3}/4 $$
Alturas de un isósceles
En un triángulo acutángulo $ ABC $, las alturas de $ B $ y $ C $ respecto a las bases $ CA $ y $ AB $, respectivamente, se intersectan en el punto $ S $. Sean $ M $ en $ AB $ y $ N $ en $ CA $ los pies de esas alturas. Demostrar que $AB=CA$ si y sólo si el ángulo $ MSB $ mide el doble que el ángulo $ CBN $.
Teorema de Napoleón (interior)
Si en un triángulo $ ABC $ se construyen triángulos equiláteros interiores sobre sus lados, entonces los centros $X, Y, Z$ de dichos triángulos equiláteros determinan un triángulo equilátero $ XYZ $, conocido como triángulo de Napoleón interior. (Demostrarlo.)
Teorema de Napoleón (exterior)
Si en un triángulo $ ABC $ se construyen triángulos equiláteros exteriores sobre sus lados, entonces los centros $X, Y, Z$ de dichos triángulos equiláteros determinan un triángulo equilátero $ XYZ $, conocido como triángulo de Napoleón exterior. (Demostrarlo.)
Dividir un segmento...
Dividir un segmento $AC$ en la razón $3/2$ (en razón de 3 a 2), internamente por un punto B y externamente por un punto $G$.
