Publicaciones Recientes
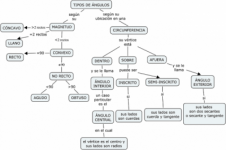
Clasificación de ángulos
Parecería que de ángulos hay muy poco que decir. Son los objetos geométricos que se miden con un transportador ¿cierto? Cierto, pero hay toda una terminología escolar que el aprendiz debería aprender.
En lo que sigue voy a hablar primero de una clasificación de los ángulos, y en la segunda parte voy plantear la clasificación de las relaciones entre dos ángulos. En cada una de esas clasificaciones se presenta primero un mapa conceptual y después se hace el mismo planteamiento pero de manera discursiva.
Problema 6, IMO 2010
Sea $a_1, a_2, a_3, \ldots$ una sucesión de números reales positivos. Se tiene que para algún entero positivo $s$,
$$a_n = \textrm{max}\{a_k + a_{n-k} \textrm{ tal que } 1 \leq k \leq n - 1\}$$
para todo $n > s$. Demuestre que existen enteros positivos $\ell$ y $N$, con $\ell \leq s$, tales que $a_n = a_\ell + a_{n-\ell}$ para todo $n \geq N$.
Problema 3, IMO 2010
Sea $\mathbb{N}$ el conjunto de los enteros positivos. Determine todas las funciones $g : \mathbb{N} \to \mathbb{N}$ tales que $$\left( g(m) + n\right) \left(m + g(n) \right) $$
es un cuadrado perfecto para todo $m, n \in \mathbb{N}$.
Problema 5, IMO 2010
En cada una de las seis cajas $B_1,B_2,B_3,B_4,B_5,B_6$ hay inicialmente sólo una moneda. Se permiten dos tipos de operaciones:
- Tipo 1: Elegir una caja no vacía $B_j$ , con $1 \leq j \leq 5$. Retirar una moneda de $B_j$ y añadir dos monedas a $B_{j+1}$.
- Tipo 2: Elegir una caja no vacía $B_k$, con $1 \leq k \leq 4$. Retirar una moneda de $B_k$ e intercambiar los contenidos de las cajas (posiblemente vacías) $B_{k+1}$ y $B_{k+2}$.
Determine si existe una sucesión finita de estas operaciones que deja a las cajas $B_1,B_2,B_3,B_4,B_5$ vacías y a la caja $B_6$ con exactamente $2010^{2010^{2010}}$ monedas. (Observe que $a^{b^c} = a^{(b^c)}$.)
Problema 2, IMO 2010
Sea $ABC$ un triángulo, $I$ su incentro y $\Gamma$ su circunferencia circunscrita. La recta $AI$ corta de nuevo a $\Gamma$ en $D$. Sean $E$ un punto en el arco $\widehat{BDC}$ y $F$ un punto en el lado $BC$ tales que
$$\angle BAF = \angle CAE < \frac{1}{2} \angle BAC.$$
Sea $G$ el punto medio del segmento $IF$. Demuestre que las rectas $DG$ y $EI$ se cortan sobre $\Gamma$.
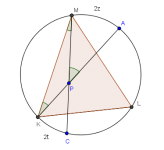
Problema 4, IMO 2010
Sea $P$ un punto en el interior del triángulo $ABC$ con circunferencia circunscrita $\Gamma$. Las rectas $AP,BP,CP$ cortan otra vez a $\Gamma$ en los puntos $K,L,M$, respectivamente. La recta tangente a $\Gamma$ en $C$ corta a la recta $AB$ en $S$. Demostrar que si $SC=SP$ entonces $MK=ML$.
Problema 1, IMO 2010
Determine todas las funciones $f : \mathbb{R} \to \mathbb{R}$ tales que $$f(\lfloor x \rfloor y)= f(x) \lfloor f(y) \rfloor$$ para todos los números $x, y \in \mathbb{R}$. ($\lfloor z\rfloor$ denota el mayor entero que es menor o igual que $z$.)
Sentido de la estructura geométrica
Chicas Fresa en Palacio
Las chicas fresa andan en Palacio de Hierro (sólo les faltan los lentes para irse de vacaciones a Los Cabos):
K: "¿Ya vieron? ¡Qué looser! ¡Son piratas! Nada que ver conmigo, yo quiero unos Carrera, Champion como los de Lady Gaga".

IMO 2010: México lugar 33
Después de que el año pasado la delegación mexicana que acudió a la Olimpiada Internacional de Matemáticas (IMO por sus siglas en inglés) se derrumbó hasta el lugar 50, en la IMO 2010 obtuvo el lugar 33 como país (con una plata y tres bronces), regresando a un nivel satisfactorio. (En los últimos 10 años, los lugares de México en la IMO han sido: 33 (2010), 50, 37, 24, 31, 37, 41, 46, 46, 32(2000).
