Problemas
También puedes compartirnos alguno de tus problemas favoritos:
Problema 4. 29a Olimpiada Mexicana de Matemáticas
Problema 3. 29a Olimpiada Mexicana de Matemáticas
- $f(1)=1$
- Para todos $a,b$ enteros positivos, se cumple que
$$f(a+b+ab)=a+b+f(ab)$$ .
Problema 2. 29a Olimpiada Mexicana de Matemáticas
Sean $n$ un entero positivo y $k$ un entero entre $1$ y $n$. Se tiene un tablero de $n \times n$ color blanco. Se hace el siguiente proceso. Se dibujan $k$ rectángulos con lados de longitud entera, con lados paralelos a los del tablero y tales que su esquina superior derecha coincide con la del tablero. Luego, estos $k$ rectángulos se rellenan de negro. Esto deja una figura blanca en el tablero. ¿Cuántas figuras blancas diferentes podemos obtener, que no se puedan obtener haciendo el proceso con menos de $k$ rectángulos?
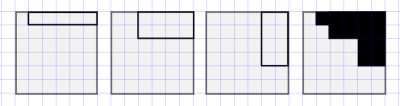
Problema 1. 29a Olimpiada Mexicana de Matemáticas
Sea $ABC$ un triángulo y sea $H$ su ortocentro. Sea $PQ$ un segmento que pasa por $H$ con $P$ en $AB$, $Q$ en $AC$ y tal que $\angle PHB=\angle CHQ$. Finalmente en el ciruncírculo del triángulo $ABC$ considera $M$ el punto medio del arco $BC$ que no contiene a $A$. Muestra que $MP=MQ$.
Problema 4(C)
En una circunferencia se marcan 60 puntos, de los cuales 30 se colorean de rojo, 20 de azul y 10 de verde. La circunferencia queda así dividida en 60 arcos y a cada uno de ellos se les asigna un número de acuerdo a la siguiente regla:
--1 si une un punto rojo con uno verde
--2 si une un punto rojo con uno azul
--3 si une un punto azul con uno verde
--0 si une dos puntos del mismo color
¿Cuál es la mayor suma posible de los números asignados a los arcos? (Justifica tu respuesta.)
Problema 3(G)
Problema 2(N)
Para un entero positivo n denotamos con S(n) la suma de los dígitos y con U(n) el dígito de las unidades. Determinar todos los enteros positivos n con la propiedad de que n=S(n)+U(n)2 (Nota: Para n=324, S(n)=9 y U(n)=4.)
Problema 1(A)
Calcula el valor de n que cumpla la siguiente ecuación: $$\frac{1+3+5+...+2n-1}{2+4+6+...+2n} = \frac{2014}{2015}$$
funciones
Una empresa se encuentra desarrollando el presupuesto para sus proximos 5 años para dichos efectos la entidad sabe con base en su experiencia que los precios de ventas estan intimamente relacionados con el comportamiento de inflacion en Mexico, tambien se conoce que el precio de venta del año anterior es de $100 por unidad y la inflacion esperada para el año siguiente es de 3.8% y que crecera a su vez un 5% cada año y que los volumenes de ventas se espera que permanezcan constantes en un millon de unidades.
Determine el funcion a utiliar
Cuales son las variables utilizadas y sus tipos
Respresente la ecuacion y de el resultdo
Año Ingresos
2015
2016
2017
2018
Problema 1 - IMO 2015 - Conjunto de puntos y mediatrices.
Decimos que un conjunto finito $\cal{S}$ de puntos en el plano es equilibrado si para cada dos puntos distintos $A$ y $B$ en $\cal{S}$ hay un punto $C$ en $\cal{S}$ tal que $AC = BC$. Decimos que $\cal{S}$ es libre de centros si para cada tres puntos distintos $A$, $B$, $C$ en $\cal{S}$ no existe ningún punto $P$ en $\cal{S}$ tal que $PA=PB=PC$.
- Demostrar que para todo $n \geq 3$ existe un conjunto de $n$ puntos equilibrado.
- Determinar todos los enteros $n \geq 3$ para los que existe un conjunto de $n$ puntos equilibrado y libre de centros.
Elemental de números --pero no trivial
Hay siete cajas numeradas del 1 al 7 y alineadas. Tú tienes 2015 tarjetas que colocas en las cajas de una por una. La primera tarjeta la colocas en la primera caja, la segunda en la segunda, hasta llegar a la séptima carta la cual colocas en la caja 7. En ese momento empiezas a colocar las tarjetas en la otra dirección colocando la carta 8 en la caja 6, la 9 en la 5, hasta llegar a la carta 13 que colocas en la caja 1. La tarjeta 14 la colocas entonces en la caja 2, y continuas así hasta que cada tarjeta haya sido distribuida. ¿En cuál caja se coloca la última tarjeta? (Justifica tu respuesta.)
Necesario organizar en casos
¿Cuántos números de 6 dígitos son tales que
- los dígitos de cada número son del conjunto $\{1,2,3,4,5\}$
- cualquier dígito que aparece en el número aparece al menos dos veces?
Ejemplo: 222133 no es admisible
Problema geométrico --no tan trivial
Sea ABCD un cuadrado unitario. Con en A y radio AB se traza el arco BD. De manera similar, con centro en B y radio BA, se traza el arco AC. Calcular el radio r del círculo $\gamma$ que es tangente a los arcos AC y BD y al lado AB del cuadrado unitario.
Razonado elemental de números
Problema 11
Tres cuadrados idénticos $ABCD, AEFG, AHIJ$ (todos etiquetados en contra de las manecillas del reloj) tienen el vértice $A$ en común y los ángulos $JAB, DAE, GAH$ son iguales. Calcular el ángulo $GBH$
Problema 10
En tierras muy lejanas había una mujer que tenía 9 hijos y los tuvo en intervalos regulares de 15 meses. El mayor de ellos tenía 6 veces la edad del menor. ¿Cuál era la edad del menor?
Problema 9
Un polígono regular de $n$ lados es seccionado en dos partes mediante un solo corte recto. Una parte es un triángulo y la otra es un polígono de $m$ lados. ¿Cómo se relacionan $m$ y $n$ ?
Problema 8
En una sucesión de 6 números, cada término después del segundo es la suma de los dos anteriores. Sabiendo que los 6 suman 13 y que el último término es cuatro veces el primero, calcula el primer término
Problema 7
Encuentra los valores de $a$ y $b$ enteros positivos en los que se cumpla que $a/5 + b/7 = 31/35$
Problema 6
180 multiplicado por un entero positivo $N$ resulta en un cubo perfecto (un número elevado al cubo). ¿Cuál es el mínimo valor posible de $N$ ?
