Problemas
También puedes compartirnos alguno de tus problemas favoritos:
¿Trazo auxiliar? OK Pero... ¿cómo lo descubres?
En un triángulo isósceles AOB, rectángulo en O, se eligen los puntos P,Q,S en los lados OB,OA,AB, respectivamente, y un punto R interior al triángulo, de tal manera que el cuadrilátero PQRS sea un cuadrado. Si la razón de áreas entre el cuadrado y el triángulo es 2/5, calcular la razón OP/OQ.
Cuadrilátero en un cubo
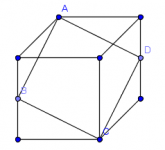
En un cubo de arista 6 los puntos medios B,D de dos aristas opuestas, y dos vértices opuestos A,C pero no en las aristas de los puntos medios B,D, forman un cuadrilátero ABCD. Encontrar el área de ese cuadrilátero.
Semicírculo y la descomposición en dos sumandos de un segmento.
Sea $$BC$ el diametro de una semicirculo y sea $A$ el punto medio del semicirculo. Sea M un punto sobre el arco $AC$. Seam $P$ y $Q$ los pies de las perpendiculares desde $A$ y C a la linea $BM$, respectivamente.
Demustra que $BP=PQ+QC$
Áreas enteras de triángulos
El área del triángulo $ ABC $ es un entero. Sobre los lados $ BC$ y $AC$ se eligen los puintos $X$ y $Y$, respectivamente. Los segmentos $AX$ y $ BY$ se cortan en un punto $P$ dentro del triángulo $ ABC $. El área de $BPX$ es 1, la de $APY$ es 2, y la de $APB$ es un entero. Encontrar el área del triángulo $ABC.$
Segmentos iguales y colinealidad
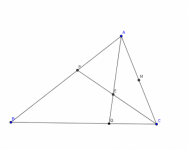
Sea ABC un triangulo, M el punto medio de CA, P el punto donde la bisectriz desde C intersecta a AB; E y Q son los puntos donde una ceviana desde A intersecta a la bisectriz y al lado BC, respectivamnete (Q no esta en la prolongacion de BC). Demuestra que los segmentos PQ y CQ son iguales, si y solo si B, E y M son colineales.
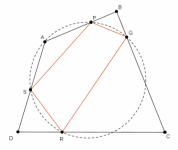
Cuadrilátero cícliclo dentro de un cuadrilátero circunscrito
Sea ABCD un cuadrilátero para el cuál existen cuatro puntos P, Q, R y S sobre los lados AB, BC, CD y DA respectivamente y tales que PB=BQ, QC = CR, RD = DS y SA = AP. Demuestra que:
- a) El cuadrilátero ABCD es circunscrito
- b) El cuadrilátero PQRS es cíclico.
IMO4_2009_invertido
Sean ABC un triángulo isósceles rectángulo en A, J su incentro y AD, BE las bisectrices de los ángulos A y B, respectivamente. La altura AD es tangente al incírculo del triángulo ADC (con incentro en I) en P y al lado CA en Q. Demostrar que:
Equilátero seccionado (3G, take_home_1)
Sea ABC un triángulo equilátero y A’, B’ , C’, puntos sobre los lados BC, CA y AB, respectivamente, tales que $$AC'/C'B=BA'/A'C=CB'/B'A=2$$ Las intersecciones de los segmentos AA’, BB’ y CC’ determinan un triángulo interior, digamos, DEF.
Una propiedad trivial de la potencia de un punto
Sean dados tres puntos distintos O, P, Q en el plano. Demostrar que OP=OQ si y sólo si P y Q tienen la misma potencia respecto a un círculo cualquiera con centro en O.
IMO 2009 Problema 2
Sean ABC un triángulo de circuncentro O, P y Q puntos sobre AB y AC, respectivamente, y K, L, M los puntos medios de BQ, CP y PQ, respectivamente. Si el circuncírculo del triangulo KLM es tangente a PQ, demostrar que OP=OQ.
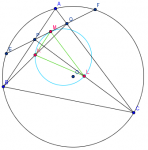
IMO 2009 Problema 4
En un triángulo $ ABC $, donde $AB=AC$, los bisectrices internas de $\angle{A}$ y $\angle{B}$ cortan a los lados $ BC $ y $AC$ en $D$ y $E$, respectivamente. Sea $I$ el incentro del triángulo $ADC$. Supongamos que $\angle{IEB}=45$. Encontrar todos los valores posibles de $\angle{A}$.

Probar isósceles
En una semicircuferenica de diámetro AB se elige un punto D y se baja una perpendicular al diámetro AB cortándolo en C. En el espacio descrito por DC, CB y el arco BD se inscribe un círculo tangente a CD en L, a BC en J y al arco BD en K. Demostrar que AD=AJ.
Potencia de un punto y circunferencias ortogonales
Sean dados una circunferencia c de radio r y centro O, y dos puntos M y M' tales que $OM\cdot OM'=r^2$ (i.e., inversos uno del otro respecto a c). Demostrar que cualquier circunferencia c' que pase por M y M' es ortogonal a c.
Condición necesaria y suficiente para cíclicos
Sea PQRS un cuadrilátero tal que sus lados opuestos PR y QS se cortan en un punto T. Demostrar que PQRS es cuadrilátero cíclico si y sólo si $TR\cdot TP=TS\cdot TQ.$
El lugar geométrico de la reflexión de un punto
Sean $ P$ un punto en el interior de una circunferencia $\mathcal{C}$ y $ M$ un punto sobre $\mathcal{C}$. Definamos $ N$ el punto sobre $\mathcal{C}$ tal que el ángulo $\measuredangle MPN = 90^{\circ}$ (en sentido contrario de las manecillas del reloj). Llamemos $P'$ el punto que resulta de reflejar $ P$ con respecto a $MN$.
Construcción de una circunferencia ortogonal
Sea dada una circunferencia $c$. Demostrar que el siguiente procedimiento produce una circunferencia ortogonal a $c$ con centro en un punto $P$ fuera de $c$.
1) Trazamos las tangentes a $c$ desde $P$ ubicando los puntos de tangencia $T$ y $T'$.
2) Trazamos la circunferencia con centro en $P$ y radio $PT$. Esta es la circunferencia ortogonal pedida.
Caracterización del eje radical
Demostrar que el eje radical de dos circunferencias es el lugar geométrico de los puntos que cumplen la propiedad de que el producto de la suma por la diferencia de sus distancias a los centros es una constante.
Valor de la potencia de un punto
Demostrar que la potencia de un punto $P$ respecto a la circunferencia $c$ con centro en $O$ y radio $ r $ es $PO^2-r^2$
Construcción del inverso
Sea dada una circunferencia c de centro O y radio r, y un punto P fuera del círculo. Demostrar que el siguiente procedimiento produce el inverso P' de P con respecto a la circunferencia c.
1) Trazar la recta OP.
2) Trazar una de las tangentes desde P a c, y llamar T al punto de tangencia.
Trazar una tangente a una circunferencia
Sea dada una circunferencia c de centro O y radio r, y un punto P fuera del círculo. Demostrar que el siguiente procedimiento produce el punto de tangencia T de la tangente que pasa por P.
1) Trazar el segmento OP.
2) Trazar la circunferencia de diámetro OP y llamar T a uno de los puntos de intersección con c.
